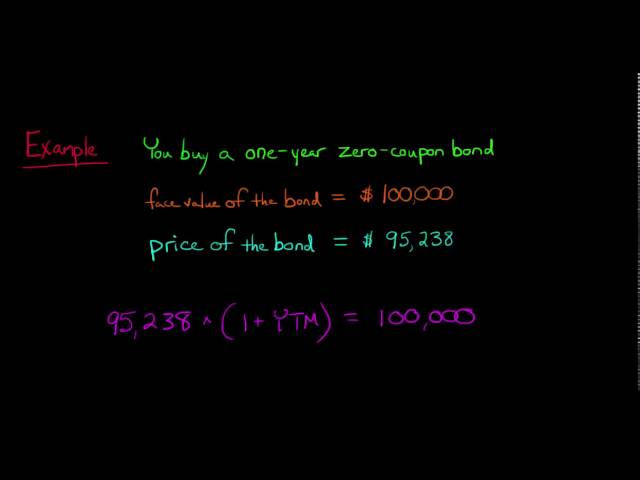Calculating yield-to-maturity (YTM) for zero-coupon bonds, a crucial aspect of fixed income analysis, involves determining the annualized rate of return on a bond that pays no coupons.
Understanding YTM for zero-coupon bonds is essential for investors seeking fixed income investments that offer capital appreciation without regular interest payments. Historically, zero-coupon bonds have attracted investors seeking long-term capital growth in a low-yield environment.
This article will comprehensively guide you through the formula and steps required to calculate YTM for zero-coupon bonds, empowering you to make informed investment decisions and maximize returns in the fixed income market.
How to Calculate YTM Zero Coupon Bond
Understanding the key aspects of calculating yield-to-maturity (YTM) for zero-coupon bonds is crucial for effective fixed income analysis and investment decisions.
- Bond Pricing
- Maturity Date
- Face Value
- Discount Rate
- Time to Maturity
- Yield Curve
- Compounding
- Tax Implications
These aspects are interconnected, influencing the calculation and interpretation of YTM. Bond pricing is determined by the present value of the bond’s future cash flows, which are discounted using the discount rate. The maturity date and time to maturity define the duration of the investment and the period over which the yield accrues. The face value represents the amount repaid at maturity, while the yield curve provides a benchmark for interest rates at different maturities. Compounding and tax implications further impact the effective yield earned by investors. Understanding these aspects enables investors to accurately calculate YTM and make informed decisions in the zero-coupon bond market.
Bond Pricing
Bond pricing lies at the heart of calculating yield-to-maturity (YTM) for zero-coupon bonds. The price of a zero-coupon bond is the present value of its future cash flow, which is the face value received at maturity. To calculate the present value, the future cash flow is discounted back to the present using an appropriate discount rate.
The discount rate is typically derived from the prevailing yield curve, which reflects market interest rates for different maturities. In essence, bond pricing involves determining the current value of the bond’s future cash flow using a discount rate that reflects the market’s assessment of risk and return.
Understanding the relationship between bond pricing and YTM is crucial for investors seeking to make informed fixed income investment decisions. The bond’s price directly influences its yield-to-maturity. A higher bond price results in a lower YTM, and vice versa. This relationship underscores the importance of accurate bond pricing in calculating YTM, as it ensures that the calculated yield reflects the actual market value of the bond.
Maturity Date
In the context of calculating yield-to-maturity (YTM) for zero-coupon bonds, the maturity date holds significant importance as a critical component. The maturity date represents the predetermined date on which the bond’s face value is repaid to the investor. It directly influences the calculation of YTM and serves as a crucial factor in determining the bond’s overall attractiveness.
The maturity date determines the time period over which the bond’s yield accrues. A longer maturity date generally implies a higher YTM, as investors demand a higher return for committing their funds for an extended period. Conversely, shorter maturity dates tend to result in lower YTMs due to the reduced risk and shorter investment horizon.
In practice, investors often consider the maturity date in conjunction with their investment goals and risk tolerance. Those seeking long-term capital appreciation may opt for bonds with distant maturity dates and potentially higher YTMs, while investors prioritizing stability and lower risk may prefer bonds with shorter maturity dates and lower YTMs. Understanding the relationship between maturity date and YTM enables investors to make informed decisions that align with their financial objectives.
Face Value
In calculating the yield-to-maturity (YTM) of a zero-coupon bond, the face value serves as a critical parameter that directly impacts the yield calculation. The face value, also known as the par value or principal, represents the amount that will be repaid to the bondholder upon maturity. Understanding its significance and various facets enables investors to accurately determine the bond’s yield and make informed investment decisions.
- Maturity Value: The face value of a zero-coupon bond is the sole payment received by the investor at the bond’s maturity. Unlike coupon bonds that make periodic interest payments, zero-coupon bonds offer a single payout at maturity, making the face value a crucial component of the bond’s return.
- Bond Price Determination: The face value serves as a reference point for determining the bond’s price in the market. The bond’s price is typically lower than its face value, reflecting the time value of money and the discounting of future cash flows back to the present.
- Yield-to-Maturity Calculation: The face value plays a central role in calculating the bond’s YTM. The YTM represents the annualized rate of return an investor can expect to earn on the bond if held until maturity. The face value, along with the bond’s price and time to maturity, is used in the YTM formula to determine this yield.
- Investment Decision-Making: Understanding the face value’s impact on YTM is essential for investors seeking to evaluate and compare different zero-coupon bond offerings. By considering the relationship between face value and yield, investors can make informed decisions that align with their investment objectives and risk tolerance.
In summary, the face value of a zero-coupon bond is a critical factor that influences the bond’s price, yield calculation, and investment decision-making. A thorough understanding of its significance and various facets empowers investors to accurately assess the potential returns and make informed choices that maximize their investment outcomes.
Discount Rate
The discount rate plays a pivotal role in the calculation of yield-to-maturity (YTM) for zero-coupon bonds, establishing a cause-and-effect relationship that is essential to understand for accurate yield determination. The discount rate represents the rate at which future cash flows are discounted back to the present to determine the bond’s current value. In the context of zero-coupon bonds, the face value received at maturity is the sole cash flow considered.
The discount rate is a critical component of YTM calculation, as it directly influences the value assigned to the future cash flow. A higher discount rate results in a lower present value of the cash flow, leading to a lower YTM. Conversely, a lower discount rate yields a higher present value and a correspondingly higher YTM. This inverse relationship highlights the importance of selecting an appropriate discount rate that accurately reflects the market’s perception of risk and return.
In practice, the discount rate is often derived from the prevailing yield curve, which represents the market interest rates for different maturities. By using the yield curve as a reference, investors can determine a reasonable discount rate that aligns with the bond’s maturity and the current market conditions. Real-life examples of discount rate application include valuing long-term government bonds, corporate bonds, and other fixed income securities that do not pay regular coupons. Understanding the relationship between discount rate and YTM empowers investors to make informed decisions when investing in zero-coupon bonds.
In summary, the discount rate is a critical factor in calculating YTM for zero-coupon bonds, influencing the present value of future cash flows and ultimately determining the bond’s yield. By understanding this relationship, investors can accurately assess the potential returns and make informed investment choices that align with their financial goals.
Time to Maturity
In the context of calculating yield-to-maturity (YTM) for zero-coupon bonds, the time to maturity holds significant importance as it represents the duration of the investment and the period over which the yield accrues. Understanding its multifaceted aspects enables investors to accurately determine the bond’s yield and make informed investment decisions.
- Maturity Date: The maturity date marks the end of the bond’s life, when the face value is repaid to the investor. It directly influences the calculation of time to maturity.
- Investment Horizon: Time to maturity defines the investor’s commitment period, aligning with their investment goals and risk tolerance. Longer maturities imply higher potential returns but also greater interest rate risk.
- Yield Curve: The prevailing yield curve provides reference points for determining appropriate discount rates based on different maturities. Time to maturity is a key factor in locating the relevant point on the yield curve.
- Present Value Calculation: In YTM calculation, time to maturity determines the number of periods over which future cash flows are discounted back to the present, using the appropriate discount rate.
In summary, time to maturity is an essential aspect of calculating YTM for zero-coupon bonds, influencing factors such as maturity date, investment horizon, yield curve analysis, and present value determination. Understanding its multifaceted implications empowers investors to make informed decisions that align with their financial objectives and risk tolerance.
Yield Curve
In the realm of fixed income investments, the yield curve plays a pivotal role in calculating the yield-to-maturity (YTM) of zero-coupon bonds. The yield curve graphically depicts the relationship between interest rates and maturities for different fixed income securities. Understanding this connection is essential for investors seeking to accurately determine the potential returns on their zero-coupon bond investments.
The yield curve serves as a benchmark for determining appropriate discount rates, which are used to calculate the present value of future cash flows. In the case of zero-coupon bonds, the face value received at maturity represents the sole cash flow. By referencing the yield curve, investors can identify the prevailing market interest rate for a specific maturity, ensuring that the discount rate used in the YTM calculation aligns with current market conditions.
For instance, if an investor is considering a 10-year zero-coupon bond, they would locate the 10-year point on the yield curve to determine the corresponding interest rate. This rate would then be used as the discount rate to calculate the present value of the face value received at maturity. By incorporating the yield curve into their analysis, investors gain a more accurate representation of the potential yield they can earn on their investment.
In summary, the yield curve is an indispensable component of calculating YTM for zero-coupon bonds. It provides investors with a reliable reference point for determining appropriate discount rates, ensuring that their yield calculations reflect current market conditions and enabling them to make informed investment decisions.
Compounding
In the context of calculating yield-to-maturity (YTM) for zero-coupon bonds, compounding plays a critical role in determining the effective yield earned over the investment period. Compounding refers to the phenomenon where interest earned in a given period is added to the principal, and interest is then earned on the increased amount in subsequent periods.
For zero-coupon bonds, which do not pay regular interest payments, compounding occurs when the face value received at maturity is reinvested at a certain rate of return. This reinvestment effectively increases the overall yield earned on the bond. The longer the time to maturity, the greater the impact of compounding, as there are more periods for interest to be earned and reinvested.
Real-life examples of compounding in YTM calculations for zero-coupon bonds include:
An investor purchases a 10-year zero-coupon bond with a face value of $1,000. If the bond’s YTM is 5%, the investor will receive $1,628.89 at maturity, assuming the reinvested interest earns the same 5% return.
Understanding the impact of compounding on YTM is crucial for investors seeking to accurately assess the potential returns on their zero-coupon bond investments. By incorporating compounding into their calculations, investors gain a more realistic representation of the yield they can expect to earn over the life of the bond. This understanding empowers them to make informed investment decisions that align with their financial goals and risk tolerance.
Tax Implications
Tax implications play a crucial role in the context of calculating yield-to-maturity (YTM) for zero-coupon bonds, as they directly impact the investor’s after-tax return. Understanding the nuances of tax implications is essential for investors seeking to accurately determine the potential returns on their zero-coupon bond investments.
For zero-coupon bonds, which do not pay regular interest payments, the entire return is realized as capital gain upon maturity. This means that investors are subject to capital gains tax on the difference between the purchase price and the face value received at maturity. The tax rate applicable depends on the investor’s individual tax bracket and the holding period of the bond.
Real-life examples illustrate the impact of tax implications on YTM calculations for zero-coupon bonds:
An investor purchases a 10-year zero-coupon bond with a face value of $1,000 and a YTM of 5%. If the investor is in the 25% tax bracket and holds the bond until maturity, the after-tax yield would be approximately 4.25%.
Understanding the practical applications of tax implications in YTM calculations empowers investors to make informed decisions that maximize their after-tax returns. By considering the tax implications associated with zero-coupon bonds, investors can adjust their investment strategies and optimize their portfolios for tax efficiency. This understanding also enables investors to compare the after-tax returns of zero-coupon bonds with other fixed income investments, such as coupon bonds or money market accounts.
Frequently Asked Questions about Calculating YTM for Zero-Coupon Bonds
This FAQ section addresses common questions and clarifications regarding the calculation of yield-to-maturity (YTM) for zero-coupon bonds.
Question 1: What is the formula for calculating YTM for a zero-coupon bond?
The formula for calculating YTM for a zero-coupon bond is: YTM = (FV / PV)^(1 / n) – 1 Where: – YTM is the yield-to-maturity – FV is the face value of the bond – PV is the present value of the bond – n is the number of years to maturity
Question 2: What is the difference between YTM and current yield?
YTM reflects the total return an investor can expect to earn on a bond held until maturity, while current yield represents the annual interest payment divided by the current market price of the bond. For zero-coupon bonds, which do not pay regular interest, YTM and current yield are the same.
Question 3: How does the time to maturity affect YTM?
YTM generally increases as the time to maturity increases. This is because investors demand a higher return for committing their funds for a longer period.
Question 4: What is the impact of compounding on YTM?
For zero-coupon bonds, compounding occurs when the face value received at maturity is reinvested at a certain rate of return. Compounding increases the overall yield earned on the bond, especially for longer maturities.
Question 5: How do taxes affect YTM?
The after-tax YTM is lower than the pre-tax YTM due to the capital gains tax incurred upon maturity. The tax implication depends on the investor’s tax bracket and the holding period of the bond.
Question 6: What is the difference between a zero-coupon bond and a coupon bond?
Unlike zero-coupon bonds, coupon bonds pay regular interest payments throughout their life. As a result, coupon bonds typically have lower YTMs than zero-coupon bonds with the same maturity.
In summary, understanding these FAQs provides a solid foundation for calculating and interpreting YTM for zero-coupon bonds. Accurately calculating YTM empowers investors to make informed investment decisions that align with their financial goals and risk tolerance.
In the next section, we will delve into advanced strategies for utilizing YTM in fixed income portfolio management.
Tips for Calculating Yield-to-Maturity for Zero-Coupon Bonds
This section provides a comprehensive set of tips to assist investors in accurately calculating the yield-to-maturity (YTM) for zero-coupon bonds, empowering them to make informed investment decisions and maximize their returns.
Tip 1: Utilize reputable sources: Refer to credible sources such as financial websites, investment firms, or bond rating agencies for accurate yield curve data.
Tip 2: Consider multiple time horizons: Calculate YTM for different time horizons to understand the potential impact of interest rate fluctuations on your investment.
Tip 3: Factor in tax implications: Determine the after-tax YTM to account for the impact of capital gains tax on your returns.
Tip 4: Reinvestment assumptions: Clearly define your assumptions for reinvesting the face value at maturity to accurately assess the impact of compounding.
Tip 5: Compare with other investments: Evaluate the YTM of zero-coupon bonds against alternative fixed income investments to make informed investment choices.
Summary: By incorporating these tips into your YTM calculations, you can enhance the precision of your yield estimates and make more informed investment decisions. Accurate YTM calculations empower investors to navigate the fixed income market effectively and achieve their financial objectives.
The following section will explore advanced strategies for utilizing YTM in fixed income portfolio management, building upon the foundation established in this section.
Conclusion
In summary, this article has provided a comprehensive guide to calculating the yield-to-maturity (YTM) for zero-coupon bonds. We have explored the fundamental concepts, formulas, and factors that influence YTM calculations, emphasizing the importance of accurate yield estimation for informed investment decisions.
Key takeaways include:
Understanding the interplay between bond pricing, maturity date, face value, discount rate, time to maturity, yield curve, compounding, and tax implications is crucial for precise YTM calculations. Utilizing reputable sources, considering multiple time horizons, factoring in tax implications, making realistic reinvestment assumptions, and comparing with other investments enhance the accuracy of YTM calculations.
Accurately calculating YTM empowers investors to navigate the fixed income market effectively. By understanding the nuances of YTM for zero-coupon bonds, investors can make informed investment choices that align with their financial goals and risk tolerance, ultimately maximizing their returns and achieving their long-term financial objectives.