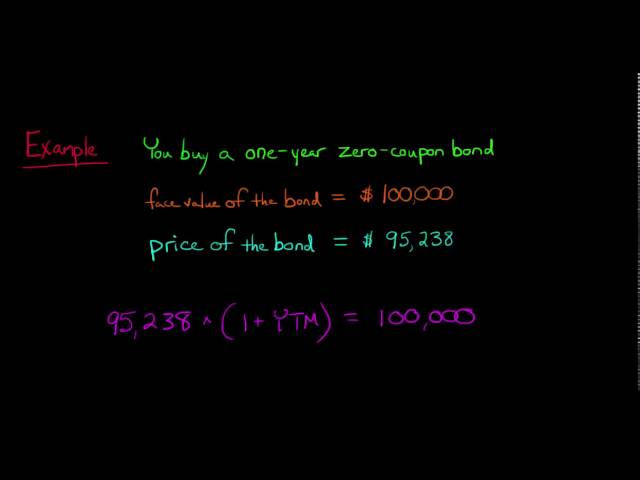Valuing zero-coupon bonds is crucial for investors seeking a secure return on their investment. A zero-coupon bond is a debt security that pays no periodic interest payments (coupons), but instead is sold at a discount to its maturity value, offering a lump sum return at the maturity date.
Understanding the calculation of zero-coupon bond values is essential for effective portfolio management. Zero-coupon bonds provide a guaranteed return and are particularly attractive during periods of low interest rates. The development of these bonds in the 1980s revolutionized the fixed-income market.
This article will delve into the calculation of zero-coupon bond values, exploring the factors that influence their pricing and providing practical guidance for investors.
How to Calculate Value of Zero Coupon Bond
Calculating the value of zero-coupon bonds requires consideration of several key aspects that influence their pricing and returns. These aspects encompass both qualitative and quantitative factors, providing a comprehensive understanding of these unique fixed-income securities.
- Maturity Date
- Face Value
- Yield to Maturity
- Discount Rate
- Time to Maturity
- Current Market Interest Rates
- Creditworthiness of the Issuer
- Tax Implications
- Inflation Expectations
- Call and Put Options
Understanding these aspects allows investors to accurately value zero-coupon bonds, assess their risk-return profile, and make informed investment decisions. By considering the interplay between these factors, investors can optimize their fixed-income portfolios and achieve their financial goals.
Maturity Date
Maturity date plays a critical role in determining the value of zero-coupon bonds. It represents the date on which the bond matures and the investor receives the face value of the bond. The longer the time to maturity, the higher the risk and the higher the yield to maturity required by investors. This is because there is a greater chance that interest rates will change over a longer period, potentially affecting the bond’s value.
To illustrate, consider two zero-coupon bonds with a face value of $1,000. Bond A has a maturity date of 5 years, while Bond B has a maturity date of 10 years. If the current market yield to maturity is 5%, Bond A will be priced at $783.53, while Bond B will be priced at $613.91. This is because investors demand a higher yield for the longer-term Bond B to compensate for the increased risk.
Understanding the relationship between maturity date and bond value is essential for investors. By considering the time to maturity and the current market interest rates, investors can make informed decisions about which zero-coupon bonds to purchase to meet their investment goals and risk tolerance.
Face Value
The face value of a zero-coupon bond represents the amount that the investor will receive at the maturity date. It is a critical component of calculating the bond’s value, as it determines the amount of return the investor will receive. The face value is also used to calculate the bond’s yield to maturity, which is a key metric used to compare the bond’s return to other investments.
For example, consider a zero-coupon bond with a face value of $1,000 and a maturity date of 10 years. If the current market yield to maturity is 5%, the bond will be priced at $613.91. This is because the investor will receive $1,000 at the end of 10 years, and the present value of that future cash flow, discounted at the yield to maturity of 5%, is $613.91.
Understanding the relationship between face value and bond value is essential for investors. By considering the face value and the current market yield to maturity, investors can make informed decisions about which zero-coupon bonds to purchase to meet their investment goals and risk tolerance.
Yield to Maturity
Yield to maturity (YTM) and value of zero-coupon bond are inextricably linked. YTM is the annual rate of return an investor can expect to receive if they hold the bond until maturity. It is a critical component of calculating the value of a zero-coupon bond, which is sold at a discount to its face value and pays no periodic interest payments.
The relationship between YTM and bond value is inverse: as YTM increases, bond value decreases, and vice versa. Consider a $1,000 face value zero-coupon bond with a maturity of 5 years. If the YTM is 5%, the bond will be priced at $783.53. If the YTM increases to 6%, the bond’s price will fall to $746.26. This is because investors require a higher return (YTM) to compensate for the lower present value of the bond’s future cash flows.
Understanding the relationship between YTM and bond value is crucial for investors. By considering the YTM and the time to maturity, investors can make informed decisions about which zero-coupon bonds to purchase to meet their investment goals and risk tolerance.
Discount Rate
In the context of “how to calculate value of zero coupon bond,” the discount rate plays a crucial role in determining the present value of future cash flows. It represents the rate at which future cash flows are discounted back to the present day, providing a basis for calculating the bond’s value.
- Required Rate of Return: The discount rate often reflects the required rate of return for investors, considering the risk and time value of money.
- Market Interest Rates: It can be influenced by prevailing market interest rates and economic conditions, which impact the opportunity cost of capital.
- Credit Risk of Issuer: The discount rate may vary based on the creditworthiness of the bond issuer, with higher risk leading to a higher discount rate.
- Time to Maturity: The discount rate considers the time period until the bond matures, as future cash flows are discounted over this period.
Understanding the concept of discount rate is essential for accurately calculating the value of zero coupon bonds. By considering the various factors that influence the discount rate, investors can make informed decisions about the pricing and suitability of these bonds within their investment portfolios.
Time to Maturity
In the realm of fixed income securities, particularly when calculating the value of zero coupon bonds, “Time to Maturity” emerges as a critical component that profoundly influences the valuation process. A zero-coupon bond, unlike its coupon-bearing counterparts, makes no periodic interest payments, offering a lump sum return at maturity. Hence, determining the present value of this future cash flow necessitates careful consideration of the time until maturity.
The relationship between “Time to Maturity” and “how to calculate value of zero coupon bond” is directly proportional. As the time to maturity increases, the present value of the bond decreases. This is because the investor must wait a longer period to receive the face value, and the uncertainty associated with future cash flows and interest rate fluctuations grows. To compensate for this extended waiting period, investors demand a higher return, leading to a higher discount rate applied to the future cash flow.
For instance, consider two zero-coupon bonds with identical face values but different maturities. Bond A matures in 5 years, while Bond B matures in 10 years. Assuming a constant discount rate, Bond A will be priced higher than Bond B, reflecting the shorter waiting period and lower uncertainty associated with its cash flow.
Understanding the connection between “Time to Maturity” and “how to calculate value of zero coupon bond” empowers investors to make informed decisions. It enables them to assess the risk-return profile of zero-coupon bonds, compare them to other fixed income investments, and optimize their portfolio allocations based on their investment horizon and risk tolerance.
Current Market Interest Rates
In the realm of fixed income securities, “Current Market Interest Rates” play a pivotal role in determining the value of zero-coupon bonds. These rates serve as the benchmark against which the future cash flows of a zero-coupon bond are discounted to calculate its present value.
The relationship between “Current Market Interest Rates” and “how to calculate value of zero coupon bond” is inversely proportional. As current market interest rates rise, the value of zero-coupon bonds falls, and vice versa. This is because higher interest rates imply a greater opportunity cost of holding a zero-coupon bond, which offers no periodic interest payments. Investors demand a higher return to compensate for this opportunity cost, leading to a decrease in the present value of the bond’s future cash flow.
For example, consider a zero-coupon bond with a face value of $1,000 and a maturity of 5 years. If the current market interest rate is 5%, the bond will be priced at $783.53. However, if the market interest rate increases to 6%, the bond’s price will fall to $746.26. This illustrates the direct impact of “Current Market Interest Rates” on the valuation of zero-coupon bonds.
Understanding this connection is crucial for investors seeking to make informed decisions about zero-coupon bonds. It enables them to assess the impact of changing interest rates on the value of their investments, make accurate yield calculations, and optimize their portfolio allocations accordingly.
Creditworthiness of the Issuer
In the realm of fixed income investments, the “Creditworthiness of the Issuer” emerges as a critical component of “how to calculate value of zero coupon bond.” It exerts a significant influence on the bond’s pricing and risk profile.
The creditworthiness of an issuer is a measure of its ability and willingness to fulfill its financial obligations, including timely payment of interest and principal. This assessment is typically performed by credit rating agencies, which assign ratings that range from AAA (highest credit quality) to D (default).
A higher credit rating generally indicates a lower risk of default, which translates into a lower yield to maturity for the zero-coupon bond. Conversely, a lower credit rating implies a higher risk of default, resulting in a higher yield to maturity to compensate investors for the increased risk. This relationship underscores the direct impact of “Creditworthiness of the Issuer” on “how to calculate value of zero coupon bond.” For example, consider two zero-coupon bonds with identical face values and maturities. If one bond is issued by a highly creditworthy issuer (e.g., AAA rating) and the other by a less creditworthy issuer (e.g., B rating), the bond issued by the former will have a lower yield to maturity, making it more valuable in the market.
Understanding this connection is crucial for investors seeking to make informed decisions about zero-coupon bonds. It enables them to assess the credit risk associated with a particular bond, evaluate its suitability within their risk tolerance, and make accurate yield calculations to optimize their portfolio returns.
Tax Implications
In the context of fixed income investing, “Tax Implications” play a significant role in “how to calculate value of zero coupon bond.” Understanding the tax treatment of zero-coupon bonds is essential for investors to make informed decisions and accurately assess their potential returns.
The primary tax implication of zero-coupon bonds is related to the timing of taxation. Unlike coupon-bearing bonds that pay periodic interest payments, zero-coupon bonds do not make any interest payments until maturity. As a result, the entire return on a zero-coupon bond is taxed as capital gains when the bond matures or is sold, rather than being spread out over the life of the bond.
This tax treatment can have a significant impact on the after-tax return of a zero-coupon bond, particularly for investors in higher tax brackets. For example, an investor in the 37% tax bracket who purchases a zero-coupon bond with a 5% yield to maturity will have an after-tax yield of only 3.15%. This is because the entire 5% return will be taxed as capital gains at maturity, resulting in a lower overall return.
Understanding the “Tax Implications” of zero-coupon bonds is critical for investors to make informed investment decisions. By considering the impact of taxes on their potential returns, investors can compare zero-coupon bonds to other fixed income investments and make choices that are aligned with their financial goals and tax situation.
Inflation Expectations
In the realm of fixed income investing, “Inflation Expectations” play a critical role in “how to calculate value of zero coupon bond.” Understanding the relationship between inflation expectations and zero-coupon bonds is essential for investors to make informed decisions and accurately assess their potential returns.
Inflation erodes the purchasing power of money over time, which can significantly impact the real return on a zero-coupon bond. When inflation expectations are high, investors demand a higher yield to maturity on zero-coupon bonds to compensate for the expected loss of purchasing power. Conversely, when inflation expectations are low, investors are willing to accept a lower yield to maturity, as the real return on their investment is expected to be higher.
For example, consider two zero-coupon bonds with identical face values and maturities. If one bond is issued during a period of high inflation expectations and the other during a period of low inflation expectations, the bond issued during the period of high inflation expectations will have a higher yield to maturity. This is because investors require a higher return to offset the expected erosion of purchasing power over the life of the bond.
Understanding the connection between “Inflation Expectations” and “how to calculate value of zero coupon bond” is critical for investors seeking to make informed investment decisions. By considering the impact of inflation expectations on their potential returns, investors can compare zero-coupon bonds to other fixed income investments and make choices that are aligned with their financial goals and inflation outlook.
Call and Put Options
In the context of fixed income securities, “Call and Put Options” play a significant role in “how to calculate value of zero coupon bond.” These options provide investors with additional flexibility and potential return opportunities, influencing the overall valuation of the bond.
A call option grants the holder the right, but not the obligation, to buy the bond at a specified price (strike price) on or before a certain date (expiration date). Conversely, a put option grants the holder the right, but not the obligation, to sell the bond at the strike price on or before the expiration date.
The presence of call and put options can affect the value of a zero-coupon bond in several ways. For instance, if interest rates rise, the value of the bond may decline. However, if the bond has a call option, the holder can exercise the option to sell the bond at the strike price, limiting their losses. Similarly, if interest rates fall, the value of the bond may increase. In this case, a put option allows the holder to lock in the higher price by selling the bond at the strike price.
Understanding the connection between “Call and Put Options” and “how to calculate value of zero coupon bond” is essential for investors seeking to make informed decisions. By considering the potential impact of these options on the bond’s value, investors can assess the risks and rewards associated with different zero-coupon bond investments and make choices that align with their investment goals and risk tolerance.
Frequently Asked Questions
This FAQ section provides concise answers to common questions regarding the calculation of zero-coupon bond values, clarifying key concepts and addressing potential concerns.
Question 1: What is the formula for calculating the value of a zero-coupon bond?
The value of a zero-coupon bond can be calculated using the formula: Present Value = Face Value / (1 + Yield to Maturity)^Time to Maturity.
Question 2: How does the yield to maturity affect the value of a zero-coupon bond?
The yield to maturity and the value of a zero-coupon bond have an inverse relationship. As the yield to maturity increases, the present value of the bond’s future cash flow decreases, resulting in a lower bond value.
Question 6: What is the impact of inflation on zero-coupon bond values?
Inflation can erode the purchasing power of the future cash flow received from a zero-coupon bond, potentially reducing its real value. Investors should consider inflation expectations when assessing the potential returns of zero-coupon bonds.
Summary:
These FAQs have highlighted the key factors influencing the calculation of zero-coupon bond values. Understanding these factors is essential for investors seeking accurate valuations and informed investment decisions.
Transition:
In the next section, we will explore advanced strategies for valuing zero-coupon bonds, including the use of yield curves and the impact of credit risk.
Tips for Calculating Zero-Coupon Bond Values
This section provides actionable tips to enhance the accuracy and efficiency of your zero-coupon bond value calculations.
Tip 1: Utilize a reputable bond pricing calculator. Online tools and software can simplify calculations and provide reliable results.
Tip 2: Consider the bond’s credit rating. The creditworthiness of the issuer significantly impacts the yield to maturity and bond value.
Tip 3: Factor in inflation expectations. Anticipated inflation rates can affect the real return on your investment.
Tip 4: Understand the impact of call and put options. These options can influence the bond’s value and potential returns.
Tip 5: Use yield curves to estimate future interest rates. Yield curves provide insights into market expectations, which can inform your yield to maturity assumptions.
Tip 6: Consider tax implications. The timing of taxation on zero-coupon bonds can affect your after-tax returns.
Tip 7: Seek professional advice if needed. For complex calculations or specific investment strategies, consulting a financial professional is recommended.
By following these tips, you can enhance your understanding of zero-coupon bond valuation and make more informed investment decisions.
In the next section, we will explore additional strategies for evaluating zero-coupon bonds, including advanced techniques and risk management considerations.
Conclusion
This comprehensive guide has delved into the intricacies of calculating the value of zero-coupon bonds, equipping investors with the knowledge and tools to make informed investment decisions. Key points to remember include the inverse relationship between yield to maturity and bond value, the significance of considering credit risk and inflation expectations, and the impact of call and put options on potential returns.
As fixed income investors navigate the evolving financial landscape, understanding the valuation of zero-coupon bonds becomes increasingly crucial. By mastering these calculation techniques and incorporating them into their investment strategies, investors can optimize their portfolios and achieve their financial goals. The insights gained from this exploration serve as a valuable foundation for further exploration and successful investing in the zero-coupon bond market.