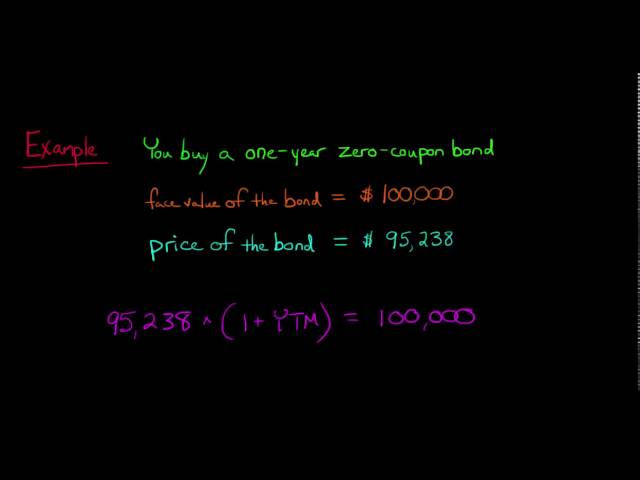Calculating the formula for zero coupon bonds, a specific type of fixed-income security that trades at a discount to its face value, is a fundamental concept in financial analysis. In the world of finance, understanding how to determine the value of these bonds is crucial for making informed investment decisions.
Zero coupon bonds offer several advantages, including low volatility, reduced default risk, and the ability to benefit from compounding returns. Historically, the introduction of zero coupon bonds in the mid-20th century revolutionized fixed-income investing by providing investors with a new avenue for capital appreciation and risk management.
This article comprehensively explores the formula for calculating the price of zero coupon bonds, covering essential concepts, practical applications, and advanced techniques for valuing these securities.
How to Calculate Zero Coupon Bond Formula
Understanding the formula for calculating zero coupon bond prices is essential for accurate valuation and informed investment decisions. This formula considers several key aspects:
- Face value
- Time to maturity
- Yield to maturity
- Compounding
- Present value
- Bond value
- Discount rate
- Current yield
- Semi-annual yield
These aspects are interconnected, and their accurate calculation is crucial for determining the fair value of zero coupon bonds. The formula takes into account the time value of money, the effect of compounding, and the relationship between bond price and yield. Understanding these aspects enables investors to make informed decisions about their fixed-income investments.
Face value
The face value of a zero coupon bond is the amount that the bondholder will receive at maturity. It is also known as the principal or par value. The face value is an important component of the zero coupon bond formula because it is used to calculate the bond’s present value. The present value is the current worth of the bond’s future cash flows, and it is used to determine the bond’s price.
For example, a zero coupon bond with a face value of $1,000 and a maturity of 10 years would have a present value of $613.91 if the yield to maturity is 5%. This means that the bond could be purchased for $613.91 today and would be worth $1,000 at maturity.
Understanding the relationship between face value and the zero coupon bond formula is important for investors because it allows them to calculate the bond’s price and make informed investment decisions. The face value is a key factor in determining the bond’s yield to maturity and its overall value.
Time to maturity
Time to maturity is a critical factor in calculating the price of a zero coupon bond. It represents the amount of time remaining until the bond matures and the investor receives the face value. Understanding the impact of time to maturity is essential for making informed investment decisions.
- Length
The length of time to maturity influences the bond’s price. Longer-term bonds are generally more sensitive to changes in interest rates and have higher price volatility. - Yield to maturity
Time to maturity also affects the bond’s yield to maturity (YTM). YTM is the annualized rate of return an investor expects to receive if they hold the bond until maturity. Longer-term bonds typically have higher YTMs due to the increased interest rate risk. - Price volatility
The price of a zero coupon bond is inversely related to time to maturity. As time to maturity decreases, the bond’s price becomes less sensitive to changes in interest rates, resulting in lower price volatility. - Callable bonds
Some zero coupon bonds are callable, meaning the issuer has the option to redeem the bond before maturity. Callable bonds typically have lower yields to maturity than non-callable bonds with similar maturities.
In summary, time to maturity is a multifaceted aspect that significantly impacts the valuation of zero coupon bonds. Investors should carefully consider the time to maturity when making investment decisions, as it affects the bond’s price, yield, volatility, and overall risk profile.
Yield to maturity
Yield to maturity (YTM) is a crucial concept in calculating the value of zero coupon bonds. It represents the annualized return an investor expects to receive if they hold the bond until maturity. YTM is a fundamental factor in determining the bond’s price and is influenced by several key aspects:
- Face value
The face value is the amount the bondholder will receive at maturity. A higher face value leads to a higher YTM. - Time to maturity
Bonds with longer maturities generally have higher YTMs due to the increased interest rate risk. - Market interest rates
YTM is heavily influenced by prevailing market interest rates. When interest rates rise, YTMs tend to increase, and vice versa. - Credit risk
Bonds issued by companies or governments with higher credit risk typically have higher YTMs to compensate investors for the increased risk of default.
Understanding the relationship between YTM and the other factors involved in calculating zero coupon bond prices is essential for investors. By considering these aspects, investors can make informed decisions about their fixed-income investments and accurately assess the potential returns and risks associated with zero coupon bonds.
Compounding
Compounding is an essential concept in calculating the formula for zero coupon bonds. It refers to the repeated earning of interest on interest over time. In the context of zero coupon bonds, compounding plays a crucial role in determining the bond’s value and yield to maturity.
Zero coupon bonds are unique in that they make no periodic interest payments. Instead, the interest is compounded over the life of the bond and paid out as a lump sum at maturity. The compounding effect allows the bond’s value to grow exponentially over time, even in the absence of regular interest payments.
The formula for calculating the price of a zero coupon bond incorporates the concept of compounding through the use of the exponential function. The formula takes into account the face value of the bond, the time to maturity, and the yield to maturity (which represents the compounded annual return). By considering the compounding effect, the formula accurately determines the present value of the bond’s future cash flow, which is the price at which the bond can be purchased in the market.
In practice, compounding has significant implications for investors. By understanding the impact of compounding on zero coupon bond prices, investors can make informed decisions about the timing of their investments, the maturity dates of the bonds they choose, and the overall yield they can expect to earn. Compound interest can significantly enhance the returns on long-term investments, making zero coupon bonds an attractive option for investors seeking capital appreciation.
Present value
Present value is a fundamental concept in finance, representing the current worth of a future sum of money. In the context of zero coupon bond valuation, present value plays a pivotal role in determining the bond’s price and yield to maturity.
The formula for calculating the price of a zero coupon bond relies on the principle of present value. It considers the face value of the bond, the time to maturity, and the yield to maturity (YTM) to calculate the present value of the bond’s future cash flow. The YTM, which represents the compounded annual return, is used to discount the face value back to the present to determine the bond’s current price.
In practice, present value is crucial for investors to understand the true value of zero coupon bonds. By calculating the present value, investors can assess the bond’s attractiveness relative to other investment options and make informed decisions about their fixed-income portfolios. Present value analysis helps investors determine the fair price to pay for a zero coupon bond and estimate the potential return on their investment.
Overall, the connection between present value and the formula for calculating zero coupon bond prices is integral to fixed-income investing. Understanding this relationship empowers investors to accurately value zero coupon bonds, assess their risk and return profiles, and make optimal investment decisions to achieve their financial goals.
Bond value
Comprehending “Bond value” is pivotal in mastering “how to calculate zero coupon bond formula”. It represents the present worth of an entity’s promise to pay its debt obligation at a specified future date. Understanding its multifaceted nature empowers investors to make informed decisions regarding their fixed-income investments.
- Face Value
The principal amount to be repaid at maturity, the foundation upon which the bond’s value is established.
- Time to Maturity
The duration until the bond matures, directly influencing its value due to market interest rate fluctuations and inflation.
- Yield to Maturity (YTM)
The annualized return an investor can expect if they hold the bond until maturity, a crucial factor in determining bond value.
- Market Conditions
External factors such as economic indicators, interest rate trends, and investor sentiment that can impact bond values.
These facets intertwine to form a holistic view of “Bond value”. By considering their collective impact, investors can accurately calculate zero coupon bond prices and make informed investment decisions. Understanding these components not only enhances the comprehension of bond valuation but also empowers investors to navigate the complexities of fixed-income investing.
Discount rate
The “Discount rate” plays a pivotal role in the formula for calculating the price of zero coupon bonds, as it represents the rate used to discount the future cash flows of the bond back to its present value. Understanding the various aspects of the discount rate and its implications is crucial for accurately valuing zero coupon bonds.
- Market interest rate
The prevailing interest rate in the market serves as a benchmark for the discount rate. It influences the present value of future cash flows and, consequently, the price of the zero coupon bond.
- Time to maturity
The longer the time to maturity of the bond, the higher the discount rate applied. This reflects the increased uncertainty and risk associated with longer-term investments.
- Credit risk
The creditworthiness of the bond issuer also impacts the discount rate. Bonds issued by entities with lower credit ratings carry a higher risk premium and, hence, a higher discount rate.
- Inflation
Inflationary expectations can affect the discount rate. Higher anticipated inflation leads to a higher discount rate, as it erodes the value of future cash flows.
By considering these facets of the discount rate, investors can gain a deeper understanding of the factors that influence the pricing of zero coupon bonds. This knowledge empowers them to make informed investment decisions and accurately assess the potential risks and returns associated with these fixed-income securities.
Current yield
Within the context of “how to calculate zero coupon bond formula,” “Current yield” is a vital concept that offers valuable insights into the potential returns and characteristics of zero coupon bonds. By examining its multifaceted nature, investors can gain a deeper understanding of these fixed-income securities and make informed investment decisions.
- Annual Interest Payment
Current yield is calculated by dividing the annual interest payment by the bond’s current market price. It provides an indication of the bond’s immediate income-generating potential. - Bond Price
The current yield is inversely related to the bond’s price. As the bond price increases, the current yield decreases, and vice versa. This relationship highlights the trade-off between current income and capital appreciation. - Time to Maturity
Current yield is also influenced by the bond’s time to maturity. Longer-term bonds typically have higher current yields due to the increased uncertainty and risk associated with longer-term investments. - Credit Risk
The creditworthiness of the bond issuer also impacts the current yield. Bonds issued by entities with lower credit ratings carry a higher risk premium, resulting in a higher current yield.
In summary, “Current yield” offers valuable insights into the income potential, price dynamics, maturity characteristics, and credit risk associated with zero coupon bonds. By understanding these facets, investors can make informed investment decisions and accurately assess the potential risks and returns of these fixed-income securities.
Semi-annual yield
In the context of zero coupon bond valuation, “Semi-annual yield” holds significant importance due to its direct relationship with the formula used to calculate the bond’s price. Zero coupon bonds are unique in that they do not pay periodic interest payments, making the semi-annual yield a crucial factor in determining their value.
The semi-annual yield represents the annualized yield of a zero coupon bond, divided into two equal payments made every six months. It is calculated by taking the square root of the bond’s yield to maturity (YTM) and subtracting one. This relationship arises from the fact that the zero coupon bond’s price is determined by discounting its future cash flows, which consist of a single payment at maturity, back to the present using the semi-annual yield.
Understanding the connection between semi-annual yield and the zero coupon bond formula is essential for accurately valuing these bonds and making informed investment decisions. By considering the semi-annual yield, investors can assess the bond’s potential return and compare it with other fixed-income securities. Moreover, comprehending this relationship enables investors to calculate the bond’s price under different market conditions and make adjustments to their investment strategies accordingly.
In summary, semi-annual yield plays a critical role in the calculation of zero coupon bond prices, providing valuable insights into the bond’s value and return potential. By understanding this relationship, investors can better evaluate and manage their fixed-income investments.
Frequently Asked Questions
This section addresses common questions and clarifications regarding the formula for calculating zero coupon bond prices.
Question 1: What is the fundamental principle behind the zero coupon bond formula?
The formula for calculating zero coupon bond prices is built on the concept of present value. It determines the current worth of the bond’s future cash flow, which consists of a single payment at maturity, using the appropriate discount rate.
Question 2: How does the time to maturity impact the zero coupon bond formula?
Time to maturity is inversely related to the bond’s price. As the time to maturity increases, the present value of the future cash flow decreases, leading to a lower bond price.
Question 3: What role does the yield to maturity (YTM) play in the formula?
The YTM represents the annualized return an investor expects to receive if they hold the bond until maturity. It is used as the discount rate to calculate the present value of the bond’s future cash flow.
Question 4: How do I interpret the semi-annual yield in relation to the zero coupon bond formula?
The semi-annual yield is calculated from the YTM and is used to determine the bond’s price over the two six-month periods before maturity. It provides insights into the bond’s short-term yield characteristics.
Question 5: How can I consider inflation when using the zero coupon bond formula?
Inflation can be incorporated into the formula by adjusting the YTM or discount rate to reflect the expected inflation rate over the bond’s life.
Question 6: What are the limitations of the zero coupon bond formula?
The formula assumes that the YTM remains constant throughout the bond’s life, which may not always be the case in practice. Additionally, it does not account for factors such as call or put options that may be embedded in the bond.
These FAQs provide a concise overview of key concepts and considerations related to the zero coupon bond formula. To further delve into the practical applications and advanced techniques, let’s explore some illustrative examples and case studies in the next section.
Tips for Calculating Zero Coupon Bond Formula
This section provides practical tips to help you accurately calculate zero coupon bond prices and make informed investment decisions. Follow these guidelines to enhance your understanding and application of the formula.
Tip 1: Understand the concept of present value. Calculate the present value of the bond’s future cash flow using an appropriate discount rate to determine its current worth.
Tip 2: Consider the time to maturity. The longer the time to maturity, the lower the bond’s price due to the higher risk and uncertainty involved.
Tip 3: Determine the yield to maturity (YTM). Use the YTM as the discount rate to calculate the present value of the bond’s future cash flow.
Tip 4: Calculate the semi-annual yield. Divide the square root of the YTM by two to determine the semi-annual yield, which is used for semi-annual compounding.
Tip 5: Incorporate inflation. Adjust the YTM or discount rate to reflect the expected inflation rate over the bond’s life.
Tip 6: Consider tax implications. Factor in any applicable taxes that may affect the bond’s return.
Tip 7: Use financial calculators or software. Utilize tools designed specifically for bond calculations to simplify the process and minimize errors.
Tip 8: Stay updated on market conditions. Monitor changes in interest rates and economic indicators to make informed decisions about investing in zero coupon bonds.
By following these tips, you can gain a deeper understanding of the zero coupon bond formula and apply it effectively to value these bonds accurately. This knowledge empowers you to make informed investment decisions and optimize your fixed-income portfolio.
Moving forward, the final section of this article will delve into advanced techniques and case studies to further enhance your understanding of zero coupon bond valuation.
Conclusion
This article has comprehensively explored the intricacies of calculating zero coupon bond prices, delving into key concepts, practical applications, and advanced techniques. By understanding the fundamental principles of present value, yield to maturity, time to maturity, and semi-annual yield, investors can accurately value these fixed-income securities and make informed investment decisions.
Key takeaways include the inverse relationship between bond price and time to maturity, the significance of yield to maturity as the discount rate, and the impact of inflation on bond valuation. These interconnected concepts provide a solid foundation for understanding zero coupon bond pricing and managing fixed-income investments.