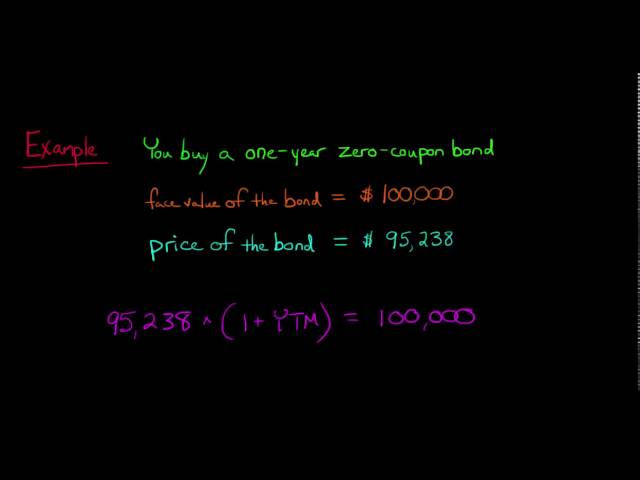Calculating zero coupon rate involves finding the discount rate that equates the present value of future cash flows to the current price of a bond. For example, a zero-coupon bond with a face value of $1,000 and a maturity of 10 years would require a zero coupon rate of around 4.65% to sell at a current price of $631.94.
Zero coupon rates are important in fixed income markets and are used to value bonds, calculate yields, and assess credit risk. They have also played a role in the development of other financial instruments, such as zero-coupon swaps and options.
In this article, we will delve into the nitty-gritty of calculating zero coupon rates, exploring different methods and considering the impact of various factors on the resulting rate.
How to Calculate Zero Coupon Rate
Determining the zero coupon rate is a crucial aspect of fixed income analysis, as it helps investors assess the present value of future cash flows and make informed investment decisions. Here are 10 key aspects to consider when calculating zero coupon rates:
- Bond Face Value
- Maturity Date
- Current Market Price
- Yield to Maturity
- Compounding Frequency
- Time to Maturity
- Future Cash Flows
- Discount Rate
- Present Value
- Bond Rating
These aspects are interconnected and influence the calculation of the zero coupon rate. For example, a bond with a higher face value will have a higher zero coupon rate than a bond with a lower face value, assuming all other factors are equal. Similarly, a bond with a longer maturity date will typically have a higher zero coupon rate than a bond with a shorter maturity date. By understanding these key aspects and their relationships, investors can accurately calculate zero coupon rates and make informed investment decisions.
Bond Face Value
Bond face value plays a pivotal role in determining the zero coupon rate. It represents the principal amount of the bond that will be repaid at maturity. A higher face value bond will have a higher zero coupon rate, assuming all other factors are equal. This is because the zero coupon rate is calculated to equate the present value of the future cash flows to the current price of the bond. A higher face value means a greater future cash flow, which in turn requires a higher zero coupon rate to equate to the current price.
For example, consider two zero-coupon bonds, each with a maturity of 10 years and a current price of $1,000. Assume that the first bond has a face value of $10,000 and the second bond has a face value of $20,000. Using the formula for calculating the zero coupon rate, we find that the first bond has a zero coupon rate of approximately 4.65%, while the second bond has a zero coupon rate of approximately 8.28%. This demonstrates the direct relationship between bond face value and zero coupon rate.
Understanding this relationship is crucial for investors in fixed income markets. It enables them to accurately value bonds, calculate yields, and assess credit risk. By considering the bond face value in conjunction with other factors, investors can make informed investment decisions and optimize their portfolios.
Maturity Date
Maturity Date plays a critical role in determining the zero coupon rate. It represents the date on which the bond matures and the face value is repaid to the investor. The relationship between maturity date and zero coupon rate is inverse, meaning that longer maturity dates typically lead to higher zero coupon rates. This is because investors require a higher return to compensate for the longer period of time they must wait to receive the face value of the bond.
For example, consider two zero-coupon bonds, each with a face value of $1,000. Assume that the first bond has a maturity of 10 years and the second bond has a maturity of 20 years. Using the formula for calculating the zero coupon rate, we find that the first bond has a zero coupon rate of approximately 4.65%, while the second bond has a zero coupon rate of approximately 6.15%. This demonstrates the inverse relationship between maturity date and zero coupon rate.
Understanding this relationship is crucial for investors in fixed income markets. It enables them to accurately value bonds, calculate yields, and assess credit risk. By considering the maturity date in conjunction with other factors, investors can make informed investment decisions and optimize their portfolios.
Current Market Price
Current Market Price plays a critical role in determining the zero coupon rate. It represents the current price at which a bond is trading in the market. The relationship between current market price and zero coupon rate is inverse, meaning that a higher current market price will result in a lower zero coupon rate, and vice versa. This is because the zero coupon rate is calculated to equate the present value of the future cash flows to the current market price of the bond.
For example, consider two zero-coupon bonds, each with a face value of $1,000 and a maturity of 10 years. Assume that the first bond has a current market price of $800 and the second bond has a current market price of $1,200. Using the formula for calculating the zero coupon rate, we find that the first bond has a zero coupon rate of approximately 6.51%, while the second bond has a zero coupon rate of approximately 3.03%. This demonstrates the inverse relationship between current market price and zero coupon rate.
Understanding this relationship is crucial for investors in fixed income markets. It enables them to accurately value bonds, calculate yields, and assess credit risk. By considering the current market price in conjunction with other factors, investors can make informed investment decisions and optimize their portfolios.
Yield to Maturity
Yield to Maturity (YTM) plays a crucial role in calculating zero coupon rates. YTM is the annual rate of return an investor can expect to receive if they hold a bond until maturity. It is closely related to the zero coupon rate, as both are used to determine the present value of future cash flows. The relationship between YTM and zero coupon rate is direct, meaning that a higher YTM will result in a higher zero coupon rate, and vice versa. This is because the zero coupon rate is calculated to equate the present value of the future cash flows to the current market price of the bond.
For example, consider a zero-coupon bond with a face value of $1,000 and a maturity of 10 years. If the YTM is 5%, then the zero coupon rate will also be approximately 5%. This means that an investor who purchases the bond for $631.94 (the present value of $1,000 received in 10 years at a discount rate of 5%) will earn a 5% annual return if they hold the bond until maturity.
Understanding the relationship between YTM and zero coupon rate is crucial for investors in fixed income markets. It enables them to accurately value bonds, calculate yields, and assess credit risk. By considering YTM in conjunction with other factors, investors can make informed investment decisions and optimize their portfolios.
Compounding Frequency
Compounding Frequency plays a crucial role in calculating zero coupon rates. It refers to the number of times per year that the interest on a bond is compounded. The relationship between compounding frequency and zero coupon rate is direct, meaning that a higher compounding frequency will result in a higher zero coupon rate. This is because the more frequently the interest is compounded, the greater the effect of compounding over the life of the bond.
To illustrate this relationship, consider two zero-coupon bonds, each with a face value of $1,000, a maturity of 10 years, and a yield to maturity of 5%. If the first bond has a compounding frequency of 1 (compounded annually), then the zero coupon rate will be approximately 4.65%. However, if the second bond has a compounding frequency of 12 (compounded monthly), then the zero coupon rate will be approximately 4.68%. This demonstrates the impact of compounding frequency on the zero coupon rate.
Understanding the relationship between compounding frequency and zero coupon rate is crucial for investors in fixed income markets. It enables them to accurately calculate yields, compare bonds with different compounding frequencies, and make informed investment decisions. By considering compounding frequency in conjunction with other factors, investors can optimize their portfolios and achieve their financial goals.
Time to Maturity
Time to Maturity is a crucial factor in calculating zero coupon rates. It represents the period between the issuance date of a bond and its maturity date when the principal is repaid. The relationship between time to maturity and zero coupon rate is generally inverse, meaning that longer time to maturity typically results in higher zero coupon rates. Understanding the role and implications of time to maturity is essential for accurate yield calculations and investment decision-making.
- Bond Duration
Bond duration measures the sensitivity of a bond’s price to changes in interest rates. Longer time to maturity generally leads to longer duration, which means that the bond’s price will be more volatile in response to interest rate fluctuations.
- Interest Rate Risk
Bonds with longer time to maturity are more exposed to interest rate risk. If interest rates rise, the value of longer-term bonds will typically decrease more significantly than shorter-term bonds.
- Yield Curve
The yield curve plots the relationship between yield to maturity and time to maturity for bonds of similar credit quality. The shape of the yield curve can influence the zero coupon rate, as it reflects market expectations about future interest rates.
In summary, time to maturity is a key consideration in calculating zero coupon rates. Longer time to maturity generally results in higher zero coupon rates, higher bond duration, and greater interest rate risk. Investors should carefully consider these factors when evaluating bonds and making investment decisions.
Future Cash Flows
In the calculation of zero coupon rates, Future Cash Flows play a crucial role in determining the present value of a bond. These cash flows are the periodic payments that an investor expects to receive over the life of the bond until maturity, when the principal amount is repaid.
- Coupon Payments
For coupon-paying bonds, regular interest payments are made at predetermined intervals. These payments are typically semi-annual, but can also be annual or quarterly.
- Maturity Value
At the end of the bond’s term, the investor receives the face value or maturity value, which represents the principal amount they initially invested in the bond.
- Callable Feature
Some bonds may have a callable feature, allowing the issuer to repay the bond before maturity. In such cases, the future cash flows will be affected by the call date and the call price.
- Default Risk
The creditworthiness of the bond issuer can impact the future cash flows. If the issuer defaults on its obligations, the investor may not receive all or part of the expected cash flows.
Understanding and accurately forecasting future cash flows are critical for investors to assess the value and risk of a bond investment. These factors directly influence the calculation of zero coupon rates and help investors make informed decisions about their fixed-income portfolio.
Discount Rate
Discount Rate plays a pivotal role in “how to calculate zero coupon rate.” It represents the rate of return an investor demands for tying up their money in a bond. A higher discount rate leads to a lower zero coupon rate, and vice versa. This inverse relationship stems from the time value of money principle, where the present value of future cash flows decreases as the discount rate increases.
Discount Rate is a critical component of calculating zero coupon rates because it determines the present value of the bond’s future cash flows, which are discounted back to the present using the formula: Present Value = Future Cash Flow / (1 + Discount Rate)^n, where n is the number of periods. By adjusting the discount rate, investors can assess the value of a bond and make informed decisions about their investments.
An example of Discount Rate in calculating zero coupon rate is a bond with a face value of $1,000, a maturity of 10 years, and a discount rate of 5%. The zero coupon rate, in this case, is approximately 4.65%. This means that the present value of the $1,000 received at maturity, discounted at 5% for 10 years, is equal to the current price of the bond.
Understanding the interrelation between Discount Rate and zero coupon rate is essential for investors. It enables them to accurately value bonds, assess their risk-return profile, and optimize their fixed income portfolios. By considering the impact of Discount Rate on zero coupon rates, investors can make informed investment decisions that align with their financial goals and risk tolerance.
Present Value
Present Value forms the cornerstone of “how to calculate zero coupon rate,” representing the current worth of future cash flows discounted back to the present using a specified rate. Understanding its multifaceted components and implications is crucial for accurate zero coupon rate calculations.
- Components of Present Value
Present Value is composed of individual cash flows, each discounted by a factor that reflects the time value of money.
- Real-Life Examples
In calculating zero coupon rates, Present Value is used to determine the current value of future interest payments and the principal repayment at maturity.
- Impact on Discount Rate
Present Value is inversely related to the discount rate used in the calculation. A higher discount rate results in a lower Present Value, and vice versa.
- Relevance to Zero Coupon Rates
The Present Value of all future cash flows, when set equal to the current market price of a zero-coupon bond, determines its zero coupon rate.
In essence, Present Value provides the foundation for calculating zero coupon rates. It enables investors to assess the current worth of future cash flows, compare bonds with different maturities and coupon structures, and make informed investment decisions in the fixed income market.
Bond Rating
Bond Rating plays a crucial role in “how to calculate zero coupon rate” as it directly affects the level of risk associated with the bond, which in turn influences the zero coupon rate. A bond rating is an assessment of the creditworthiness of a bond issuer, indicating the likelihood that the issuer will fulfill its financial obligations. Higher-rated bonds are considered less risky, while lower-rated bonds are considered riskier.
When calculating zero coupon rates, investors consider the bond rating to determine the appropriate discount rate. A higher bond rating typically results in a lower discount rate, as investors are less likely to demand a high return for lending to a creditworthy issuer. Conversely, a lower bond rating typically leads to a higher discount rate, as investors require a higher return to compensate for the increased risk of default.
For example, a zero-coupon bond issued by the U.S. Treasury with a maturity of 10 years and a bond rating of AAA might have a zero coupon rate of 2.5%, while a similar bond issued by a corporation with a bond rating of BB might have a zero coupon rate of 5%. This difference in zero coupon rates reflects the higher risk associated with the corporate bond.
Understanding the connection between bond rating and zero coupon rate is critical for investors, as it enables them to assess the risk-return profile of a bond investment. By considering the bond rating in conjunction with other factors, investors can make more informed decisions about which bonds to include in their portfolios.
FAQs on How to Calculate Zero Coupon Rate
This section provides answers to frequently asked questions related to calculating zero coupon rates, addressing common concerns and clarifying important aspects.
Question 1:What is the formula for calculating zero coupon rate?
Answer: The formula for calculating zero coupon rate is: Zero Coupon Rate = [(Face Value / Current Price)^(1 / Years to Maturity)] – 1
Question 2:How does maturity affect zero coupon rate?
Answer: Maturity has an inverse relationship with zero coupon rate. Longer maturities typically result in higher zero coupon rates due to increased interest rate risk and the time value of money.
Question 3:What is the impact of face value on zero coupon rate?
Answer: Face value has a direct relationship with zero coupon rate. Higher face values lead to higher zero coupon rates, as the present value of future cash flows increases.
Question 4:How is zero coupon rate related to bond rating?
Answer: Bond rating is inversely related to zero coupon rate. Higher-rated bonds have lower zero coupon rates due to lower default risk, while lower-rated bonds have higher zero coupon rates due to increased risk.
Question 5:What is the difference between zero coupon rate and yield to maturity?
Answer: Zero coupon rate is the internal rate of return for a zero-coupon bond, while yield to maturity is the annualized rate of return for a bond with periodic coupon payments.
Question 6:How can I use zero coupon rates to value bonds?
Answer: Zero coupon rates can be used to value bonds by discounting the future cash flows (face value) back to the present using the zero coupon rate as the discount rate.
These FAQs provide a concise overview of key considerations when calculating zero coupon rates. Understanding these concepts is essential for accurate yield calculations, bond valuation, and informed investment decisions in the fixed income market.
In the next section, we will delve deeper into advanced techniques for calculating zero coupon rates, considering factors such as compounding frequency, day count conventions, and callable bonds.
Tips on Calculating Zero Coupon Rates
To ensure accurate and reliable zero coupon rate calculations, consider the following practical tips:
Tip 1: Use precise input data. Verify that the values for face value, maturity date, and current market price are correct.
Tip 2: Select the appropriate compounding frequency. Consider the frequency at which interest is compounded over the bond’s life.
Tip 3: Employ accurate day count conventions. Different conventions, such as 30/360 or actual/actual, can affect the calculation.
Tip 4: Account for callable bonds. If the bond has a call feature, adjust the calculation to reflect the potential early repayment.
Tip 5: Utilize financial calculators or software. Dedicated tools can simplify the calculation process and enhance accuracy.
Tip 6: Consider tax implications. Zero coupon bonds may have unique tax implications depending on the jurisdiction.
Tip 7: Monitor market conditions. Changes in interest rates and credit spreads can impact zero coupon rates.
Tip 8: Consult with financial professionals. Seek guidance from experienced advisors to ensure a comprehensive understanding of zero coupon rate calculations.
By implementing these tips, investors can enhance the accuracy of their zero coupon rate calculations, leading to more informed investment decisions.
In the concluding section, we will explore advanced applications of zero coupon rate calculations, including their use in yield curve construction and risk management strategies.
Conclusion
This comprehensive exploration of “how to calculate zero coupon rate” has illuminated key concepts and provided practical techniques for accurate yield computations. The article emphasized the interplay between various factors, including face value, maturity, current market price, and bond rating, in determining zero coupon rates.
Two main points emerged. Firstly, understanding the relationship between these factors and zero coupon rates empowers investors to make informed decisions about bond investments. Secondly, employing precise input data, selecting appropriate compounding frequencies and day count conventions, and considering callable bonds are crucial for accurate calculations. By incorporating these considerations, investors can gain a deeper understanding of fixed income market dynamics and optimize their investment strategies.