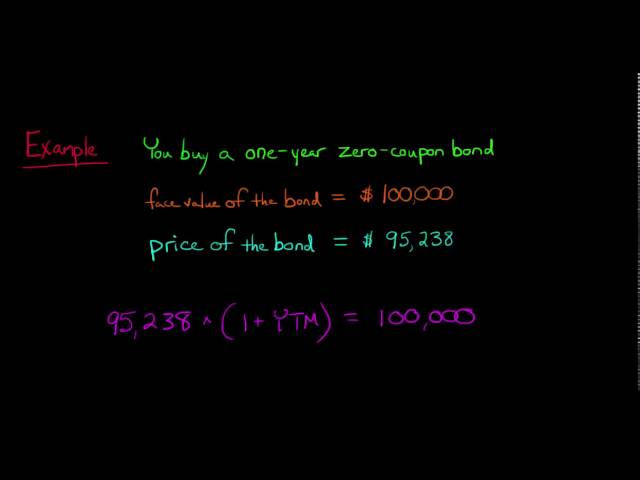Determining the Zero Coupon Yield Curve: A Comprehensive Guide
The yield curve plays a crucial role in understanding the long-term borrowing costs for governments and corporations. It is used to price bonds, determine interest rates, and assess the health of an economy. The zero-coupon yield curve is a specialized type of yield curve that considers the yield rates of zero-coupon bonds, which are bonds that pay no interest but are sold at a discount to their face value.
Understanding how to calculate the zero-coupon yield curve is essential for investors and financial analysts. This detailed guide will provide you with step-by-step instructions on calculating the zero-coupon yield curve, exploring its significance, and discussing its applications in the financial marketplace.
how to calculate zero coupon yield curve
Understanding the intricacies of calculating the zero coupon yield curve is essential for navigating the complexities of the financial markets. This involves grasping key aspects such as:
- Discounting
- Maturity
- Par value
- Bond pricing
- Interest rates
- Yield to maturity
- Interpolation
- Bootstrapping
- Market conditions
These aspects are interconnected and provide a comprehensive framework for determining the zero coupon yield curve. By delving into each aspect, investors and analysts can gain a deeper understanding of the factors that influence bond yields and make informed decisions in the financial markets.
Discounting
Discounting is a critical component of calculating the zero coupon yield curve. It involves determining the present value of future cash flows, taking into account the time value of money and the prevailing interest rates. In the context of zero-coupon bonds, discounting plays a crucial role in determining the bond’s price and yield.
To illustrate, consider a zero-coupon bond with a face value of $1,000 and a maturity of 5 years. If the current market interest rate is 5%, the present value of the bond’s future cash flow (i.e., the $1,000 face value) can be calculated using the discounting formula:
Present Value = $1,000 / (1 + 0.05)^5 = $783.53
This means that the bond should be priced at $783.53 today to reflect its future value of $1,000 at maturity. The yield to maturity (YTM) of the bond can then be calculated as the annualized rate that equates the present value to the bond’s price.
In practice, discounting is applied throughout the process of calculating the zero coupon yield curve. It enables investors and analysts to compare bonds with different maturities and determine the implied forward rates for future periods. This understanding is essential for making informed decisions in the financial markets.
Maturity
Maturity, in the context of calculating the zero coupon yield curve, holds immense significance. It represents the remaining time until a bond reaches its final payment date, directly influencing its price and yield. Understanding the nuances of maturity is essential for constructing an accurate yield curve, enabling investors to make well-informed decisions.
- Time to Expiration: Maturity signifies the duration until a bond matures, impacting its present value and yield-to-maturity calculations.
- Bond Pricing: Bonds with longer maturities generally carry higher interest rates, leading to higher prices compared to shorter-term bonds.
- Yield Curve Construction: Maturity serves as a crucial factor in plotting the zero coupon yield curve, with yields varying across different maturity dates.
- Interest Rate Risk: Bonds with longer maturities are more susceptible to interest rate fluctuations, posing higher risks for investors.
In essence, maturity plays a pivotal role in determining the value and risk profile of zero-coupon bonds. By considering the interplay between maturity and other factors such as discounting and market conditions, investors can effectively calculate the zero coupon yield curve and make informed investment choices aligned with their risk tolerance and financial goals.
Par Value
Par value, a significant concept in fixed-income markets, holds particular relevance in calculating the zero coupon yield curve. It represents the face value or redemption amount of a bond at maturity, serving as a benchmark for various calculations and yield curve constructions.
- Nominal Value: Par value represents the bond’s initial principal amount, usually indicated on the bond certificate.
- Maturity Value: At maturity, investors receive the par value, marking the repayment of the principal amount.
- Bond Pricing: Par value serves as a reference point for determining bond prices, which fluctuate based on market conditions and interest rates.
- Yield Calculations: Zero-coupon bonds, lacking periodic interest payments, rely on par value and maturity date for yield calculations, directly influencing the shape of the yield curve.
In summary, par value plays a crucial role in calculating the zero coupon yield curve, impacting bond pricing, yield computations, and the overall yield curve construction. Understanding its various facets is essential for accurate yield curve determination and informed investment decisions.
Bond pricing
Bond pricing is a fundamental aspect in calculating the zero-coupon yield curve, as it involves determining the present value of future cash flows generated by bonds. Understanding how bond pricing is determined is crucial for constructing an accurate yield curve.
- Face value: The nominal or par value of a bond represents the amount that will be repaid at maturity. It serves as a reference point for calculating bond prices and yields.
- Time to maturity: The time remaining until a bond reaches its maturity date significantly influences its price. Longer-term bonds generally have higher yields and prices than shorter-term bonds.
- Interest rates: Prevailing interest rates in the market play a major role in determining bond prices. Bonds with higher interest rates tend to trade at higher prices than those with lower interest rates.
- Credit risk: The creditworthiness of the bond issuer affects its perceived risk and, consequently, its price. Bonds issued by higher-risk issuers typically have higher yields and lower prices than those issued by lower-risk issuers.
These factors collectively determine bond prices, which are then used to calculate the zero-coupon yield curve. The yield curve, in turn, provides valuable insights into the market’s expectations of future interest rates and economic conditions.
Interest rates
Interest rates and zero coupon yield curves are inextricably intertwined, with interest rates serving as a linchpin in the calculation and interpretation of yield curves. Zero-coupon bonds, lacking periodic interest payments, heavily rely on prevailing interest rates to determine their prices and yields. The interplay between these two concepts is fundamental to understanding the financial markets and making informed investment decisions.
Interest rates directly influence the pricing of zero-coupon bonds. Higher interest rates generally lead to lower bond prices, as investors demand higher returns to compensate for the opportunity cost of investing in bonds instead of other interest-bearing assets. Conversely, lower interest rates tend to result in higher bond prices, as investors are willing to pay a premium for the fixed returns offered by bonds.
The zero-coupon yield curve is a graphical representation of the relationship between interest rates and maturities. It plots the yields of zero-coupon bonds with different maturities, providing a snapshot of the market’s expectations of future interest rates. The shape of the yield curve can reveal valuable insights into economic conditions and investor sentiment. For instance, an upward-sloping yield curve typically indicates expectations of rising interest rates, while a downward-sloping curve suggests expectations of falling interest rates.
In practical applications, understanding the connection between interest rates and zero coupon yield curves is essential for various financial activities, including portfolio management, risk assessment, and economic forecasting. Investors utilize yield curves to make informed decisions about bond investments, while policymakers rely on them to gauge market expectations and calibrate monetary policy.
Yield to maturity
Yield to maturity (YTM) holds a critical position in the calculation of the zero-coupon yield curve. It represents the annualized rate of return an investor expects to receive by holding a bond until its maturity date. Understanding the connection between YTM and the zero-coupon yield curve is crucial for accurate yield curve construction and informed investment decisions.
In practical terms, YTM serves as a benchmark for comparing the yields of zero-coupon bonds with different maturities. By plotting the YTMs of zero-coupon bonds across a range of maturities, investors can visualize the zero-coupon yield curve. This curve provides insights into the market’s expectations of future interest rates and the term structure of interest rates.
The calculation of the zero-coupon yield curve relies heavily on YTM. By equating the present value of a zero-coupon bond’s future cash flows to its market price, investors can solve for the bond’s YTM. This process, known as bootstrapping, allows for the construction of a complete yield curve that reflects market expectations of future interest rates.
Understanding the connection between YTM and the zero-coupon yield curve empowers investors to make informed decisions regarding bond investments, interest rate risk management, and portfolio optimization. By considering the interplay between YTM and the yield curve, investors can navigate the fixed-income markets with greater precision and confidence.
Interpolation
Interpolation plays a crucial role in the calculation of the zero coupon yield curve. It allows us to estimate the yield rates for maturities that do not have a corresponding zero-coupon bond. This is achieved by using mathematical techniques to interpolate between the yields of existing zero-coupon bonds.
Interpolation is necessary because the zero-coupon yield curve is not always complete. There may be gaps in the data due to the lack of zero-coupon bonds with certain maturities. Interpolation techniques bridge these gaps and provide a continuous yield curve that can be used for various financial applications.
A common interpolation method used in the context of zero-coupon yield curve calculation is linear interpolation. This method assumes a linear relationship between the yields of adjacent zero-coupon bonds and interpolates the yield for the desired maturity based on this assumption. More sophisticated interpolation techniques, such as spline interpolation, can also be employed to achieve higher accuracy.
Understanding the practical applications of interpolation in zero-coupon yield curve calculation is crucial for fixed-income investors and analysts. It enables them to estimate yield rates for maturities that are not directly observable, which is essential for pricing bonds, managing interest rate risk, and making informed investment decisions.
Bootstrapping
Bootstrapping is a numerical method used to calculate the zero-coupon yield curve. It involves iteratively solving for the yield rates of zero-coupon bonds with different maturities until the calculated prices match the observed market prices. This process is based on the assumption that the market prices of zero-coupon bonds accurately reflect the true yield rates.
Bootstrapping is a critical component of calculating the zero-coupon yield curve because it allows us to estimate the yield rates for maturities that do not have a corresponding zero-coupon bond. This is important because the zero-coupon yield curve is a continuous function that represents the yield rates for all maturities, not just those with existing zero-coupon bonds.
In practice, bootstrapping is typically performed using a computer program. The program starts with an initial guess for the yield rates of all maturities. It then iteratively solves for the yield rates until the calculated prices match the observed market prices. This process is repeated until the yield rates converge to a solution.
Understanding the practical applications of bootstrapping in calculating the zero-coupon yield curve is crucial for fixed-income investors and analysts. It enables them to estimate yield rates for maturities that are not directly observable, which is essential for pricing bonds, managing interest rate risk, and making informed investment decisions.
Market conditions
In the context of calculating the zero coupon yield curve, market conditions play a significant role in shaping the yield rates and the overall shape of the curve. These conditions reflect the prevailing economic environment, investor sentiment, and supply and demand dynamics in the bond market.
- Economic growth: Economic growth expectations influence interest rates and, subsequently, the yield curve. Strong economic growth typically leads to higher interest rates and a steeper yield curve, as investors demand higher returns on their investments.
- Inflation: Inflation expectations also impact the yield curve. Higher inflation erodes the real value of fixed income payments, leading to higher yields demanded by investors. Consequently, an anticipated rise in inflation can result in an upward shift of the yield curve.
- Interest rate policies: Central banks’ interest rate policies have a direct impact on the yield curve. Changes in policy rates influence the overall level of interest rates in the economy, affecting the yields of zero-coupon bonds and the shape of the yield curve.
- Supply and demand: The supply and demand for zero-coupon bonds also influence the yield curve. Increased demand for these bonds, driven by investors seeking safe-haven assets or hedging against interest rate risk, can lead to higher prices and lower yields.
Understanding market conditions and their impact on the zero coupon yield curve is crucial for investors and analysts when making informed decisions about fixed-income investments. By considering the interplay between economic factors, investor sentiment, and market dynamics, they can better assess the risk and return profiles of zero-coupon bonds and position their portfolios accordingly.
FAQs on Calculating the Zero Coupon Yield Curve
This section addresses common questions and clarifies aspects related to calculating the zero coupon yield curve.
Question 1: What is the significance of the zero coupon yield curve?
Answer: The zero coupon yield curve serves as a benchmark for pricing fixed-income securities and assessing interest rate expectations. It enables investors to compare yields across different maturities and make informed investment decisions.
Question 2: How is the zero coupon yield curve constructed?
Answer: The zero coupon yield curve is typically constructed using methods like bootstrapping or interpolation. These methods involve solving for the yields of zero-coupon bonds with various maturities, ensuring consistency with observed market prices.
Question 3: What factors influence the shape of the zero coupon yield curve?
Answer: The shape of the zero coupon yield curve is influenced by factors such as economic growth, inflation expectations, central bank policies, and supply and demand dynamics in the bond market.
Question 4: How can I use the zero coupon yield curve in practice?
Answer: The zero coupon yield curve has practical applications in bond pricing, interest rate risk management, and portfolio optimization. It helps investors understand the relationship between yield and maturity and make informed decisions.
Question 5: What are the limitations of the zero coupon yield curve?
Answer: While the zero coupon yield curve provides valuable insights, it relies on certain assumptions and may not fully capture all market dynamics. It is essential to consider the limitations and use the yield curve in conjunction with other market indicators.
Question 6: How can I stay updated on changes in the zero coupon yield curve?
Answer: Monitoring financial news, economic data, and central bank announcements can help you stay informed about changes in the zero coupon yield curve and the broader fixed-income market.
These FAQs provide a concise overview of the key concepts and considerations related to calculating the zero coupon yield curve. In the following section, we will delve deeper into practical applications and strategies for utilizing the yield curve in investment decision-making.
Tips for Calculating the Zero Coupon Yield Curve
This section provides practical tips to enhance your understanding and accuracy when calculating the zero coupon yield curve.
Tip 1: Grasp the underlying concepts: Before embarking on calculations, ensure a thorough understanding of discounting, maturity, and yield-to-maturity.
Tip 2: Leverage technology: Utilize spreadsheet software or specialized tools designed for yield curve calculations, as manual computations can be complex and time-consuming.
Tip 3: Choose appropriate interpolation methods: Select interpolation techniques that align with the available data and desired precision. Linear interpolation is a common starting point, while more advanced methods may be necessary for specific applications.
Tip 4: Consider market conditions: Incorporate economic indicators and market sentiment into your analysis, as these factors can significantly influence the shape and level of the yield curve.
Tip 5: Validate your results: Cross-check your calculations using different methods or compare them to published yield curves from reputable sources.
Tip 6: Monitor ongoing changes: Stay informed about economic data, central bank announcements, and market news, as these can lead to shifts in the yield curve.
Tip 7: Understand the limitations: Recognize that the zero coupon yield curve is a simplified representation of the bond market and may not capture all complexities.
By following these tips, you can enhance the accuracy and efficiency of your zero coupon yield curve calculations, enabling you to make informed investment decisions.
These practical tips provide a solid foundation for utilizing the zero coupon yield curve in your investment analysis. In the concluding section, we will explore advanced strategies for incorporating the yield curve into portfolio management and risk management.
Conclusion
In summary, calculating the zero coupon yield curve involves understanding fundamental concepts such as discounting, maturity, and yield-to-maturity. Various methods and techniques, including bootstrapping and interpolation, are employed to determine the yield rates for maturities that do not have corresponding zero-coupon bonds.
This article has highlighted the significance of market conditions, encompassing economic growth, inflation expectations, interest rate policies, and supply and demand dynamics, in shaping the zero coupon yield curve. Practical tips and strategies have been provided to enhance the accuracy and efficiency of yield curve calculations.