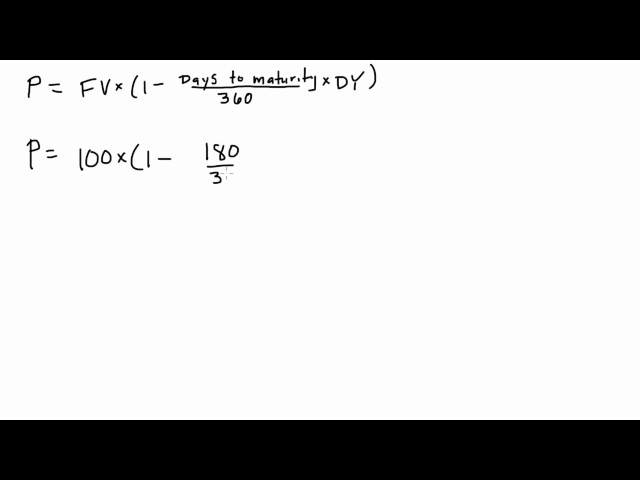Calculating the discount rate of a treasury bill is the process of determining the rate at which a bill is sold below its face value. For example, if a $1,000 treasury bill is sold for $980, the discount rate is 2%.
The discount rate is important because it determines the yield an investor will receive on a treasury bill. Treasury bills are considered very safe investments, so their yields are typically lower than those of other types of investments. However, the discount rate can still be a significant factor in determining the overall return on an investment.
Historically, treasury bills have been used as a way to finance government spending. In the United States, the first treasury bills were issued in 1890. Today, treasury bills are considered to be one of the most important financial instruments in the world.
How to Calculate Discount Rate of Treasury Bill
The discount rate of a treasury bill is a crucial factor in determining the yield an investor will receive. There are several key aspects to consider when calculating the discount rate of a treasury bill:
- Face value
- Purchase price
- Maturity date
- Days to maturity
- Current yield
- Annualized yield
- Bank discount rate
- True discount rate
- Effective annual yield
By understanding these key aspects, investors can accurately calculate the discount rate of a treasury bill and make informed investment decisions.
Face Value
The face value of a treasury bill is the amount of money that the bill will be worth at maturity. It is also the amount of money that the investor will receive when the bill matures. The face value is an important component of how to calculate the discount rate of a treasury bill because it is used to determine the amount of interest that the investor will earn on the bill.
For example, let’s say that an investor purchases a $1,000 treasury bill with a maturity date of one year. If the discount rate is 2%, the investor will pay $980 for the bill. When the bill matures, the investor will receive $1,000. The difference between the purchase price and the face value is the amount of interest that the investor will earn on the bill. In this case, the investor will earn $20 in interest.
The face value of a treasury bill is a critical component of how to calculate the discount rate because it determines the amount of interest that the investor will earn on the bill. Investors should always consider the face value of a treasury bill before purchasing it.
Purchase price
The purchase price is the second critical component of how to calculate the discount rate of a treasury bill. The purchase price is the price that the investor pays for the bill. The purchase price is important because it affects the amount of interest that the investor will earn on the bill. The lower the purchase price, the higher the interest rate that the investor will earn.
For example, let’s say that an investor purchases a $1,000 treasury bill with a maturity date of one year. If the purchase price is $980, the discount rate will be 2%. However, if the purchase price is $970, the discount rate will be 3%. As you can see, the lower the purchase price, the higher the discount rate. In addition to determining the amount of interest that the investor will earn, the purchase price also affects the yield-to-maturity (YTM) of the treasury bill.
The YTM is the annualized rate of return that the investor will earn on the treasury bill. The YTM is calculated by taking into account the purchase price, the face value, and the maturity date of the bill. The higher the purchase price, the lower the YTM. Conversely, the lower the purchase price, the higher the YTM.
Understanding the relationship between the purchase price and the discount rate of a treasury bill is critical for investors. By considering both the purchase price and the discount rate, investors can make more informed investment decisions.
Maturity date
The maturity date is the final date on which a treasury bill (T-bill) reaches its maturity. It is an important factor in calculating the discount rate, which is the difference between the purchase price and the face value of the T-bill. The discount rate is used to determine the yield, which is the return an investor will receive on the T-bill.
The maturity date is a critical component in calculating the discount rate because it determines the length of time that the investor will hold the T-bill. The longer the maturity date, the higher the discount rate and yield will be. Conversely, the shorter the maturity date, the lower the discount rate and yield will be.
For example, consider two T-bills with the same face value of $1,000. One T-bill has a maturity date of one year, while the other T-bill has a maturity date of six months. If the discount rate for the one-year T-bill is 2%, the investor will pay $980 for the T-bill. When the T-bill matures, the investor will receive $1,000, resulting in a yield of 2%. In contrast, if the discount rate for the six-month T-bill is 1%, the investor will pay $990 for the T-bill. When the T-bill matures, the investor will receive $1,000, resulting in a yield of 1%.
Understanding the relationship between the maturity date and the discount rate is essential for investors. By considering both the maturity date and the discount rate, investors can make more informed investment decisions.
Days to maturity
Days to maturity is a crucial aspect in calculating the discount rate of a treasury bill. It represents the number of days until the bill reaches its maturity date, which is when it expires and the investor receives the face value. Understanding days to maturity is essential for determining the yield and return on investment.
- Actual days
Actual days refer to the exact number of calendar days until the bill matures. This calculation considers weekends and holidays, providing an accurate measure of the time remaining.
- 30/360 convention
The 30/360 convention is a common method used to calculate days to maturity. It assumes that all months have 30 days and a year has 360 days. This simplified approach is often used for convenience and consistency.
- Impact on yield
Days to maturity significantly impact the yield of a treasury bill. Generally, bills with longer days to maturity have higher yields, as investors are compensated for lending their money for a more extended period.
- Relationship with discount rate
Days to maturity is inversely related to the discount rate. As days to maturity increase, the discount rate decreases, and vice versa. This relationship is crucial for investors to understand as it affects the overall return on their investment.
In summary, days to maturity is a critical factor in determining the discount rate and yield of a treasury bill. By considering the actual days, using the 30/360 convention, understanding its impact on yield, and recognizing its relationship with the discount rate, investors can make informed decisions and optimize their returns.
Current yield
Current yield is a critical component of how to calculate the discount rate of a treasury bill. It is the annualized rate of return that an investor would receive if they held the bill until maturity. The current yield is calculated by dividing the annual interest payment by the current market price of the bill. For example, if a $1,000 treasury bill with a maturity date of one year is selling for $980, the current yield would be 2%.
The current yield is important because it provides investors with a way to compare the yields of different treasury bills. It also allows investors to track the changes in the yield of a particular treasury bill over time. For example, if the current yield of a one-year treasury bill increases from 2% to 3%, it means that the value of the bill has decreased. This is because investors are now demanding a higher yield to compensate them for the risk of holding the bill until maturity.
The current yield is a valuable tool for investors who are considering purchasing treasury bills. By understanding the current yield, investors can make informed decisions about which bills to buy and how long to hold them.
Annualized yield
Annualized yield is a critical component of how to calculate the discount rate of a treasury bill. It is the annual rate of return that an investor would receive if they held the bill until maturity. The annualized yield is calculated by dividing the annual interest payment by the purchase price of the bill. For example, if a $1,000 treasury bill with a maturity date of one year is purchased for $980, the annualized yield would be 2%.
The annualized yield is important because it provides investors with a way to compare the yields of different treasury bills. It also allows investors to track the changes in the yield of a particular treasury bill over time. For example, if the annualized yield of a one-year treasury bill increases from 2% to 3%, it means that the value of the bill has decreased. This is because investors are now demanding a higher yield to compensate them for the risk of holding the bill until maturity.
The annualized yield is a valuable tool for investors who are considering purchasing treasury bills. By understanding the annualized yield, investors can make informed decisions about which bills to buy and how long to hold them.
Bank discount rate
The bank discount rate is the interest rate charged by a bank to its customers for short-term loans. It is a critical component of how to calculate the discount rate of a treasury bill, which is the difference between the purchase price and the face value of the bill. The bank discount rate is used to determine the yield-to-maturity (YTM) of a treasury bill, which is the annualized rate of return that an investor will receive if they hold the bill until maturity.
When the bank discount rate increases, the discount rate of treasury bills also increases. This is because investors are now demanding a higher yield to compensate them for the increased cost of borrowing money. Conversely, when the bank discount rate decreases, the discount rate of treasury bills also decreases. This is because investors are now willing to accept a lower yield in exchange for the lower cost of borrowing money.
For example, if the bank discount rate is 2%, the discount rate of a one-year treasury bill might be 1.9%. This means that an investor who purchases the bill for $980 will receive $1,000 at maturity, resulting in a yield of 2%. If the bank discount rate then increases to 3%, the discount rate of the one-year treasury bill might increase to 2.9%. This means that an investor who purchases the bill for $970 will receive $1,000 at maturity, resulting in a yield of 3%.
Understanding the relationship between the bank discount rate and the discount rate of treasury bills is important for investors. By considering both the bank discount rate and the discount rate of treasury bills, investors can make more informed investment decisions.
True discount rate
The true discount rate is a critical component in calculating the discount rate of a treasury bill. It is the annualized rate of return that an investor would receive if they purchased the bill at a discount and held it until maturity. The true discount rate is calculated by dividing the difference between the face value and the purchase price of the bill by the number of days until maturity and then multiplying by 360. Unlike the bank discount rate, which is based on a 360-day year, the true discount rate considers the actual number of days until maturity.
- Present value
The present value is the current value of a future sum of money, discounted at a specific interest rate. In the context of treasury bills, the present value is the purchase price of the bill. By considering the present value, investors can determine the true cost of the bill and calculate the true discount rate.
- Time to maturity
Time to maturity refers to the number of days until the bill reaches its maturity date. This factor is crucial in calculating the true discount rate because it determines the length of time over which the investor will earn interest. A longer time to maturity typically results in a higher true discount rate.
- Face value
The face value of a treasury bill is the amount that the investor will receive when the bill matures. By comparing the face value to the purchase price, investors can determine the discount and calculate the true discount rate. A higher face value relative to the purchase price leads to a higher true discount rate.
- Simple interest
Simple interest is calculated based on the principal amount, the interest rate, and the time period. In the case of treasury bills, the true discount rate is a form of simple interest, where the interest is calculated on the present value of the bill over the time to maturity.
Understanding the components and implications of the true discount rate enables investors to make informed decisions when calculating the discount rate of treasury bills. By considering the present value, time to maturity, face value, and the simple interest nature of the true discount rate, investors can accurately determine the yield and return on their investment.
Effective annual yield
Effective annual yield (EAY) is a critical component in calculating the discount rate of a treasury bill. It represents the annualized rate of return an investor would receive if they held the bill until maturity, taking into account the effect of compounding interest. Understanding the connection between EAY and the discount rate is essential for investors seeking accurate yield calculations and informed investment decisions.
The discount rate is the difference between the purchase price and the face value of a treasury bill. It determines the yield an investor will earn on the bill. EAY, on the other hand, considers the impact of compounding over the holding period. Compounding refers to the reinvestment of interest earned, leading to exponential growth in the investment’s value.
To illustrate, let’s consider a one-year treasury bill with a face value of $1,000. If the purchase price is $980 and the annual interest rate is 2%, the simple interest earned over the year would be $20. However, EAY takes into account that the interest earned is reinvested at the same rate, resulting in a slightly higher yield. In this case, the EAY would be approximately 2.02%, indicating a marginally higher return compared to the simple interest calculation.
Understanding the relationship between EAY and the discount rate is crucial for investors to accurately assess the yield and make informed investment decisions. By considering the impact of compounding, investors can determine the true annualized return on their treasury bill investments. This knowledge enables them to optimize their investment strategies and maximize returns.
Frequently Asked Questions
This FAQ section provides answers to common questions and clarifications regarding the calculation of the discount rate for treasury bills.
Question 1: What is the formula for calculating the discount rate of a treasury bill?
Answer: Discount Rate = (Face Value – Purchase Price) / (Face Value x Days to Maturity / 360)
Question 2: How does the maturity date affect the discount rate?
Answer: A longer maturity date generally results in a higher discount rate as investors require higher compensation for lending their funds over an extended period.
Question 3: What is the difference between the discount rate and the yield-to-maturity?
Answer: The discount rate is the upfront discount applied to the face value of the bill, while the yield-to-maturity considers the compounding effect of interest payments over the life of the bill.
Question 4: How can I calculate the effective annual yield (EAY) of a treasury bill?
Answer: EAY = (1 + (Discount Rate x Days to Maturity / 360))^360 / Days to Maturity
Question 5: What factors should I consider when comparing discount rates of different treasury bills?
Answer: Key factors to compare include maturity dates, face values, and current market conditions to determine the most favorable investment option.
Question 6: How does the bank discount rate impact the discount rate of treasury bills?
Answer: Changes in the bank discount rate can influence the demand for treasury bills and subsequently affect their discount rates.
Summary: These FAQs provide essential insights into the calculation and interpretation of discount rates for treasury bills. By understanding these concepts, investors can make informed decisions when investing in these instruments.
Transition: To delve deeper into the nuances of treasury bill pricing and its implications, let’s explore the factors that influence their discount rates.
Tips for Calculating Discount Rates of Treasury Bills
This section provides practical tips to help you accurately calculate discount rates for treasury bills and make informed investment decisions.
Tip 1: Use the correct formula
Employ the precise formula to determine the discount rate: Discount Rate = (Face Value – Purchase Price) / (Face Value x Days to Maturity / 360)
Tip 2: Consider the maturity date
Longer maturities generally result in higher discount rates due to the extended lending period and associated risk.
Tip 3: Calculate the effective annual yield (EAY)
EAY provides a more accurate measure of return by incorporating the impact of compounding over the investment period.
Tip 4: Compare discount rates across bills
Evaluate different treasury bills based on their maturity dates, face values, and current market conditions to identify the most favorable options.
Tip 5: Monitor market conditions
Stay informed about changes in the bank discount rate and economic factors that may influence treasury bill pricing and discount rates.
Summary: By following these tips, you can enhance the accuracy of your discount rate calculations and make well-informed investment decisions when investing in treasury bills.
Transition: Understanding how to calculate discount rates is crucial for maximizing returns on treasury bill investments. The final section will delve into strategies for optimizing your treasury bill portfolio.
Conclusion
Calculating the discount rate of a treasury bill is crucial for maximizing returns on investment. This article has provided insights into the key components and considerations involved in this calculation, such as the face value, purchase price, maturity date, and effective annual yield (EAY).
Understanding the relationship between these factors allows investors to accurately determine the yield they will receive and make informed investment decisions. By employing the correct formula, considering the maturity date, calculating the EAY, and monitoring market conditions, investors can enhance the accuracy of their discount rate calculations and optimize their treasury bill portfolio.