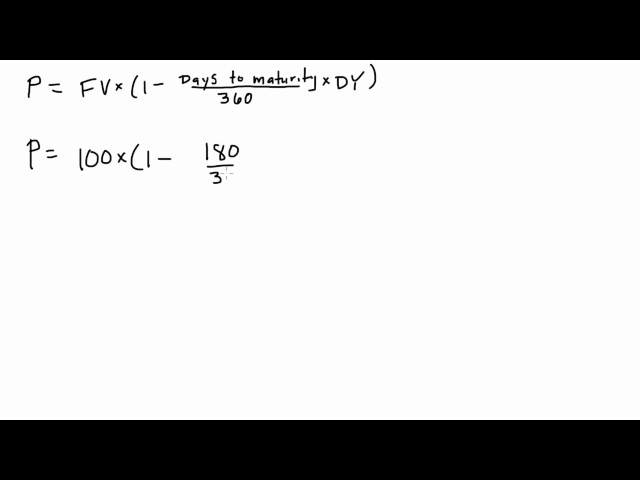The discount rate formula for Treasury bills, a fundamental formula in finance, determines the present value of a Treasury bill (T-bill). T-bills are short-term government securities that mature in one year or less. The formula is crucial when calculating the yield-to-maturity of a T-bill, a key indicator of its attractiveness to investors.
The discount rate formula plays a vital role in the financial markets by providing a standard method to compare the yields of T-bills with alternative investments. It helps investors make informed decisions about their portfolio allocations and enables governments to manage their debt effectively. Historically, the discount rate has been used by central banks to influence short-term interest rates and control inflation.
This article will delve into the details of the discount rate formula for Treasury bills, exploring its components, variations, and applications in the financial world.
Discount Rate Formula Treasury Bill
The discount rate formula for Treasury bills plays a crucial role in the financial markets. Its key aspects encompass various dimensions, including:
- Calculation
- Present value
- Yield-to-maturity
- Investment decision
- Government debt management
- Monetary policy
- Inflation control
- Risk assessment
Understanding these aspects is essential for investors, financial analysts, and policymakers. The discount rate formula provides a standardized method to compare the yields of Treasury bills with other investments, enabling informed portfolio allocation decisions. It also assists governments in managing their debt effectively and central banks in influencing short-term interest rates and controlling inflation. Furthermore, the formula helps investors assess the risk associated with Treasury bills and make informed investment decisions.
Calculation
Calculation is a crucial aspect of the discount rate formula for Treasury bills. The formula, which determines the present value of a T-bill, requires precise calculation to determine the yield-to-maturity, a key indicator of the T-bill’s attractiveness to investors. The calculation involves considering several factors, including the face value of the T-bill, the time to maturity, and the prevailing market interest rates.
The calculation of the discount rate formula for Treasury bills is a critical component of investment decision-making. Investors rely on the accuracy of the calculation to determine the potential return on their investment and compare it with alternative investments. Additionally, governments and central banks use the calculation to manage their debt and influence short-term interest rates.
A real-life example of the calculation of the discount rate formula for Treasury bills is the issuance of a 12-month T-bill with a face value of $100,000. If the prevailing market interest rate is 5%, the calculation would determine the present value of the T-bill to be approximately $95,238.10. This calculation helps investors assess the yield-to-maturity of the T-bill, which in this case would be approximately 5%.
Understanding the calculation of the discount rate formula for Treasury bills is essential for informed investment decisions, effective government debt management, and sound monetary policy. The precise calculation of the formula ensures accurate yield-to-maturity determinations, enabling investors to make optimal investment choices and governments to manage their debt effectively.
Present value
Present value is a crucial concept within the discount rate formula for Treasury bills. It refers to the current worth of a future sum of money, taking into account the time value of money and the prevailing interest rates. Understanding present value is essential for accurately determining the yield-to-maturity of T-bills and making informed investment decisions.
- Calculation: Present value is calculated using the discount rate formula, which considers the face value of the T-bill, the time to maturity, and the market interest rate.
- Time value of money: Present value recognizes that money available today is worth more than the same amount in the future due to its earning potential.
- Investment decisions: By comparing the present value of a T-bill with other investment options, investors can determine the most attractive investment opportunities.
- Yield-to-maturity: The present value of a T-bill directly influences its yield-to-maturity, which is a key indicator of the T-bill’s return on investment.
In summary, present value is a fundamental concept that enables investors to evaluate the worth of future cash flows in the context of Treasury bills. It provides a standardized method for comparing T-bills with other investments and making informed decisions.
Yield-to-maturity
Yield-to-maturity (YTM) is a critical component of the discount rate formula for Treasury bills. It represents the annualized rate of return an investor can expect to receive if they hold a Treasury bill until its maturity date. The YTM is directly influenced by the discount rate, which is the interest rate used to calculate the present value of the Treasury bill.
The relationship between YTM and the discount rate formula is reciprocal. A higher discount rate results in a lower YTM, and vice versa. This is because the discount rate is used to discount the future cash flows of the Treasury bill back to its present value. A higher discount rate will reduce the present value of these cash flows, resulting in a lower YTM.
Real-life examples of YTM within the discount rate formula for Treasury bills are abundant. For instance, if an investor purchases a one-year Treasury bill with a face value of $100,000 and a discount rate of 5%, the YTM would be approximately 5%. This means that the investor can expect to receive a return of 5% per year if they hold the Treasury bill until maturity.
Understanding the connection between YTM and the discount rate formula for Treasury bills is crucial for investors. It enables them to make informed decisions about their investments and compare the yields of different Treasury bills. Additionally, it helps investors assess the risk associated with Treasury bills and make informed portfolio allocation decisions.
Investment decision
Investment decision plays a critical role within the discount rate formula for Treasury bills. It refers to the process of evaluating and selecting Treasury bills for investment, considering factors such as risk tolerance, investment horizon, and financial goals. The discount rate formula serves as a fundamental tool in making informed investment decisions about Treasury bills.
The discount rate formula provides investors with a standardized method to calculate the present value of a Treasury bill, which is essential for determining its yield-to-maturity. The yield-to-maturity represents the annualized rate of return an investor can expect to receive if they hold the Treasury bill until maturity. By comparing the yield-to-maturity of different Treasury bills, investors can make informed decisions about which investments align with their financial objectives.
Real-life examples of investment decisions within the discount rate formula for Treasury bills are prevalent. For instance, an investor with a low-risk tolerance and a short investment horizon might opt for a short-term Treasury bill with a lower yield-to-maturity. Conversely, an investor with a higher risk tolerance and a longer investment horizon might choose a longer-term Treasury bill with a higher yield-to-maturity.
Understanding the connection between investment decision and the discount rate formula for Treasury bills empowers investors to make informed choices about their investments. It enables them to assess the risk and return characteristics of Treasury bills and align their investments with their financial goals. Furthermore, it provides a framework for evaluating the potential return on investment and making sound investment decisions.
Government debt management
Government debt management plays a critical role within the discount rate formula for Treasury bills. It refers to the strategies and techniques employed by governments to manage their outstanding debt, including Treasury bills. The discount rate formula is a fundamental tool used in government debt management to determine the present value and yield-to-maturity of Treasury bills.
By utilizing the discount rate formula, governments can effectively manage their debt by assessing the cost of borrowing and making informed decisions about the issuance and redemption of Treasury bills. The formula provides a framework for evaluating the impact of different interest rate scenarios on the government’s debt obligations and enables governments to optimize their debt portfolio.
Real-life examples of government debt management within the discount rate formula for Treasury bills are evident in various countries. For instance, the U.S. Treasury Department regularly issues Treasury bills with different maturities to manage the government’s debt. The discount rate used in the formula is determined by market conditions and influences the yield-to-maturity of Treasury bills.
Understanding the connection between government debt management and the discount rate formula for Treasury bills is crucial for policymakers and financial analysts. It provides insights into the government’s borrowing strategy, enables informed decision-making, and contributes to the overall stability of the financial system. This understanding also empowers investors to assess the risk and return characteristics of Treasury bills and make informed investment decisions.
Monetary policy
Monetary policy plays a pivotal role within the realm of discount rate formula treasury bill. It encompasses the strategies and instruments employed by central banks and governments to manage the money supply, interest rates, and inflation within an economy. Understanding monetary policy is crucial for grasping the broader context and implications of the discount rate formula treasury bill.
- Interest rate control
Monetary policy directly influences interest rates, including the discount rate used in the formula, which in turn affects the yield-to-maturity of Treasury bills. Central banks can implement expansionary or contractionary monetary policies to stimulate or curb economic activity.
- Inflation management
Monetary policy targets inflation control to maintain price stability. By managing interest rates and the money supply, central banks aim to keep inflation within a desired range, which influences the attractiveness of Treasury bills as an inflation-hedging instrument.
- Financial stability
Monetary policy contributes to financial stability by ensuring the smooth functioning of financial markets. Central banks use tools such as open market operations to manage liquidity and prevent financial crises, which can impact the demand for Treasury bills.
- Economic growth
Monetary policy aims to foster economic growth by setting appropriate interest rates that encourage investment and consumption. The discount rate formula treasury bill is a tool used to evaluate the potential return on investment in Treasury bills, considering the interplay between interest rates and economic growth.
In conclusion, monetary policy is a multifaceted aspect that significantly influences the discount rate formula treasury bill. By controlling interest rates, managing inflation, ensuring financial stability, and promoting economic growth, monetary policy shapes the environment in which Treasury bills are issued and traded. Understanding the intricacies of monetary policy is essential for investors, policymakers, and financial analysts to make informed decisions and assess the potential impact on the Treasury bill market.
Inflation control
Inflation control plays a critical role within the discount rate formula treasury bill. Inflation refers to a sustained increase in the general price level of goods and services in an economy over time. Monetary authorities, typically central banks, use various tools, including the discount rate, to control inflation and maintain price stability. The discount rate is the interest rate charged to commercial banks and other financial institutions for short-term loans from the central bank. It serves as a benchmark for other interest rates in the economy, including the yield-to-maturity of Treasury bills.
By controlling inflation, central banks can directly influence the attractiveness of Treasury bills as an investment. When inflation is low and stable, investors are more likely to invest in Treasury bills because the real return on their investment is preserved. Conversely, when inflation is high and volatile, investors may be hesitant to invest in Treasury bills due to the risk of negative real returns. The discount rate formula treasury bill, therefore, provides a mechanism for investors to assess the potential impact of inflation on their investment decisions.
Real-life examples of inflation control within the discount rate formula treasury bill are evident in various economies. For instance, the U.S. Federal Reserve uses a dual mandate of price stability and maximum employment to guide its monetary policy decisions. By managing inflation through the adjustment of the discount rate, the Federal Reserve aims to maintain a stable economic environment that supports both price stability and job creation.
Understanding the connection between inflation control and the discount rate formula treasury bill empowers investors, policymakers, and financial analysts to make informed decisions. It provides a framework for evaluating the potential impact of inflation on the Treasury bill market and enables investors to adjust their investment strategies accordingly. Furthermore, it contributes to the overall stability of the financial system by ensuring that inflation remains within manageable levels.
Risk assessment
Risk assessment is a critical aspect of the discount rate formula treasury bill, as it helps investors, policymakers, and financial analysts evaluate the potential risks associated with investing in Treasury bills. By identifying and assessing these risks, investors can make informed decisions about their investments and manage their portfolios effectively.
- Interest rate risk
Interest rate risk refers to the potential for changes in interest rates to impact the value of a Treasury bill. When interest rates rise, the value of existing Treasury bills with lower interest rates may decline, leading to potential losses for investors. - Inflation risk
Inflation risk refers to the potential for inflation to erode the real value of returns from a Treasury bill. When inflation is high, the purchasing power of the fixed interest payments from a Treasury bill may decrease, resulting in lower real returns for investors. - Credit risk
Credit risk refers to the risk that the issuer of a Treasury bill may default on its obligation to pay interest and principal. Although Treasury bills are considered very low credit risk investments, it is still a factor to consider, especially when investing in Treasury bills issued by countries with weaker credit ratings. - Liquidity risk
Liquidity risk refers to the risk that an investor may not be able to sell a Treasury bill quickly and at a fair price. While Treasury bills are generally considered highly liquid, there may be times when market conditions make it difficult to sell Treasury bills without incurring significant losses.
Understanding and assessing these risks is essential for investors to make informed investment decisions. By considering the potential risks associated with Treasury bills, investors can develop appropriate investment strategies and manage their risk exposure effectively.
Discount Rate Formula Treasury Bill FAQs
This FAQ section provides concise answers to frequently asked questions and clarifies key aspects related to the discount rate formula for Treasury bills. These questions address common concerns and misconceptions, empowering readers with a deeper understanding of this important financial concept.
Question 1: What is the discount rate formula for Treasury bills?
Answer: The discount rate formula for Treasury bills is: Present Value = Face Value / (1 + Discount Rate x Time to Maturity)
Question 2: How is the discount rate used to calculate the yield-to-maturity of a Treasury bill?
Answer: The yield-to-maturity is calculated as the annualized rate of return an investor can expect to receive if they hold a Treasury bill until maturity. It is directly influenced by the discount rate used in the formula.
Question 3: What factors can affect the discount rate for Treasury bills?
Answer: The discount rate for Treasury bills is influenced by various factors, including economic conditions, inflation expectations, and the overall demand and supply dynamics in the Treasury bill market.
Question 4: How is the discount rate formula used in government debt management?
Answer: Governments use the discount rate formula to determine the cost of borrowing and make informed decisions about the issuance and redemption of Treasury bills, contributing to effective debt management and fiscal policy.
Question 5: What is the relationship between the discount rate formula and monetary policy?
Answer: The discount rate formula is closely tied to monetary policy, as central banks use the discount rate as a tool to influence interest rates and manage the money supply, which can impact the yield-to-maturity of Treasury bills.
Question 6: How can the discount rate formula help investors?
Answer: By understanding the discount rate formula, investors can evaluate the potential return on investment in Treasury bills, assess risk, and make informed investment decisions that align with their financial goals and risk tolerance.
These FAQs provide a concise overview of the discount rate formula for Treasury bills, addressing common questions and highlighting its significance in various financial contexts. Understanding these concepts empowers investors, policymakers, and financial analysts to make well-informed decisions and navigate the Treasury bill market effectively.
In the following sections, we will delve deeper into the practical applications of the discount rate formula, exploring real-world examples and case studies to further enhance comprehension and provide actionable insights.
Treasury Inflation-Protected Securities (TIPS) Tips
This section provides actionable tips to help investors maximize the benefits and mitigate the risks associated with investing in Treasury Inflation-Protected Securities (TIPS). By implementing these strategies, investors can enhance their portfolio performance and achieve their financial objectives.
Tip 1: Understand TIPS’ unique characteristics: TIPS are inflation-linked securities that protect investors from the erosive effects of inflation. They offer a real return, which is adjusted based on changes in the Consumer Price Index (CPI).
Tip 2: Diversify your TIPS portfolio: To reduce risk and enhance returns, consider diversifying your TIPS portfolio across different maturities. This strategy helps mitigate the impact of interest rate fluctuations and inflation volatility.
Tip 3: Consider TIPS mutual funds or ETFs: For added diversification and convenience, consider investing in TIPS mutual funds or exchange-traded funds (ETFs). These funds provide exposure to a basket of TIPS, reducing individual security risk.
Tip 4: Monitor inflation expectations: Keep an eye on inflation forecasts and economic data to gauge the potential impact on TIPS. When inflation expectations rise, TIPS tend to perform well, while they may underperform during periods of low or deflationary expectations.
Tip 5: Assess your risk tolerance: TIPS are generally considered low-risk investments; however, they are not immune to market fluctuations. Determine your risk tolerance and invest in TIPS accordingly.
Tip 6: Consider your investment horizon: TIPS are suitable for both short-term and long-term investment horizons. Match the maturity of your TIPS investments with your financial goals and risk tolerance.
Tip 7: Rebalance your TIPS portfolio: Regularly review and rebalance your TIPS portfolio to maintain your desired risk and return profile. Adjust the allocation of TIPS and other assets based on market conditions and your financial objectives.
Tip 8: Consult a financial advisor: For personalized advice and guidance on TIPS investing, consider consulting a qualified financial advisor. They can help you navigate the complexities of TIPS and develop a tailored investment strategy.
By following these tips, investors can harness the benefits of TIPS and mitigate potential risks. TIPS offer a unique opportunity to protect against inflation and enhance portfolio diversification, making them a valuable addition to any investment portfolio.
In the concluding section, we will discuss the role of TIPS in a comprehensive investment strategy, exploring how they complement other asset classes and contribute to overall portfolio resilience.
Conclusion
The exploration of the discount rate formula for Treasury bills has illuminated its significance in financial markets and investment strategies. The formula serves as a cornerstone for determining the present value and yield-to-maturity of Treasury bills, enabling investors to make informed decisions about their investments.
Key insights from this article include the formula’s role in government debt management, monetary policy, and inflation control. It provides a framework for evaluating the risk and return characteristics of Treasury bills, empowering investors to assess their potential impact on their portfolios. Furthermore, the article highlights the importance of understanding the discount rate formula in the broader context of investment decision-making and financial planning.
As the financial landscape continues to evolve, a comprehensive understanding of the discount rate formula for Treasury bills remains crucial for investors, policymakers, and financial analysts. It provides a valuable tool for navigating the intricacies of the Treasury bill market, making informed investment choices, and managing risk effectively.