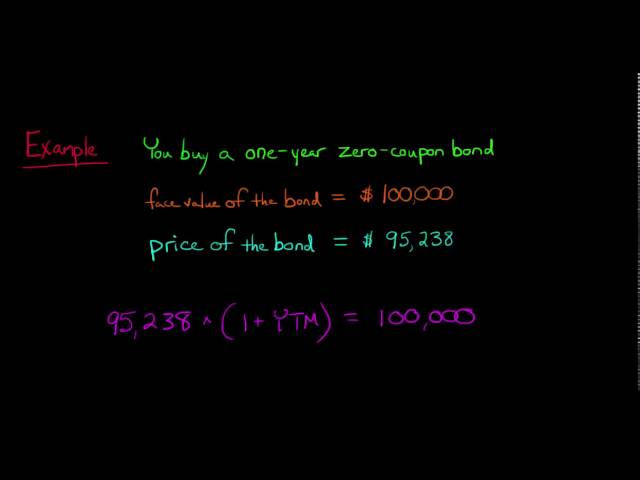Zero Coupon Bond Pricing: A Comprehensive Guide
A zero coupon bond is a type of fixed income security that pays no coupons (interest) during its life. Instead, it is issued at a deep discount to its face value and redeems at face value at maturity. For example, a $1,000 zero-coupon bond maturing in 10 years might be issued at $500, and the investor would receive $1,000 at maturity.
Zero-coupon bonds are attractive to investors because they offer a number of benefits, including simplicity, tax deferral, and potential for higher returns. They are also often used in corporate finance and structured products.
How to Calculate the Zero Coupon Bond
Zero coupon bonds are a type of fixed income security that pays no coupons (interest) during its life. Instead, it is issued at a deep discount to its face value and redeems at face value at maturity. Calculating the zero coupon bond price is important because it helps investors determine the yield and return they can expect from the bond.
- Face value
- Maturity date
- Yield to maturity
- Current price
- Time to maturity
- Accrued interest
- Callable date
- Put date
These factors all play a role in determining the price of a zero coupon bond. For example, a bond with a higher face value will be worth more than a bond with a lower face value. Similarly, a bond with a longer maturity date will be worth less than a bond with a shorter maturity date. By understanding these factors, investors can make informed decisions about whether or not to invest in zero coupon bonds.
Face value
The face value of a zero coupon bond is the amount of money that the bondholder will receive at maturity. It is also the amount of money that the bond issuer borrows from the bondholder. The face value is an important component of how to calculate the zero coupon bond price. The formula for calculating the price of a zero coupon bond is:
Price = Face value / (1 + yield)^(time to maturity)
As you can see, the face value is the numerator in this equation. This means that the higher the face value, the higher the price of the bond. For example, a $1,000 zero coupon bond with a 5% yield and a 10-year maturity will have a price of $613.91. If the face value of the bond were $2,000, the price would be $1,227.82.
It is important to note that the face value of a zero coupon bond is not the same as its market value. The market value of a bond can fluctuate depending on interest rates and other factors. However, the face value is a fixed amount that will not change.
Maturity date
The maturity date is the date on which a bond matures and the bondholder receives the face value of the bond. It is an important component of how to calculate the zero coupon bond price because it determines the amount of time that the investor will have to wait to receive the face value of the bond. The formula for calculating the price of a zero coupon bond is:
Price = Face value / (1 + yield)^(time to maturity)
As you can see, the maturity date is the denominator in this equation. This means that the longer the maturity date, the lower the price of the bond. For example, a $1,000 zero coupon bond with a 5% yield and a 10-year maturity will have a price of $613.91. If the maturity date of the bond were 20 years, the price would be $453.27.
It is important to note that the maturity date of a bond is not the same as its call date. The call date is the date on which the bond issuer can redeem the bond before maturity. If a bond is called, the bondholder will receive the face value of the bond plus any accrued interest. The call date is not a factor in how to calculate the zero coupon bond price.
Yield to maturity
Yield to maturity (YTM) is a key input in calculating the price of a zero coupon bond. It represents the annual rate of return an investor can expect to receive if they hold the bond until maturity. YTM is calculated using the following formula:
YTM = (FV / PV)^(1/n) – 1
Where:
- FV is the face value of the bond
- PV is the present value of the bond
- n is the number of years to maturity
YTM is an important consideration for investors because it allows them to compare the returns of different bonds. For example, a bond with a higher YTM will provide a higher return than a bond with a lower YTM. However, it is important to note that YTM is only an estimate of the return an investor can expect to receive. The actual return may vary depending on interest rates and other factors.
Current price
The current price of a bond is a critical input in calculating the zero coupon bond price. This is because the current price is the present value of all future cash flows that the bond is expected to generate. To calculate the zero coupon bond price, we use the following formula:
Price = Face value / (1 + yield)^(time to maturity)
As you can see, the current price is the numerator in this equation. This means that the higher the current price, the higher the price of the bond. For example, a $1,000 zero coupon bond with a 5% yield and a 10-year maturity will have a price of $613.91. If the current price of the bond were $650, the price of the bond would be $683.21.
It is important to note that the current price of a bond is not the same as its face value. The face value is the amount of money that the bondholder will receive at maturity. The current price is the amount of money that the bondholder would receive if they sold the bond today.
Time to maturity
Time to maturity is a critical component of how to calculate the zero coupon bond price. The time to maturity is the length of time until the bond matures and the bondholder receives the face value of the bond. The longer the time to maturity, the lower the price of the bond. This is because the investor has to wait longer to receive the face value of the bond, so they require a higher yield to compensate for the additional risk.
For example, a $1,000 zero coupon bond with a 5% yield and a 10-year maturity will have a price of $613.91. If the time to maturity of the bond were 20 years, the price would be $453.27. This is because the investor has to wait longer to receive the face value of the bond, so they require a higher yield to compensate for the additional risk.
Time to maturity is also an important factor to consider when investing in zero coupon bonds. Investors who need to access their money sooner should invest in bonds with shorter maturities. Investors who are willing to wait longer to receive their money can invest in bonds with longer maturities and earn a higher yield.
Accrued interest
Accrued interest refers to the interest on a bond that has accumulated but has not yet been paid to the bondholder. In the context of zero coupon bonds, accrued interest is an important factor to consider when calculating the bond’s price.
- Calculation
Accrued interest is calculated by multiplying the bond’s face value by the annual coupon rate and the number of days since the last coupon payment. For zero coupon bonds, the annual coupon rate is zero, so the accrued interest is always zero. - Impact on price
Accrued interest has no impact on the price of a zero coupon bond. This is because the bond’s price is determined solely by the face value, yield to maturity, and time to maturity.
Accrued interest is an important concept to understand when investing in zero coupon bonds. While it does not affect the bond’s price, it can affect the investor’s return. If an investor buys a zero coupon bond before the next coupon payment date, they will not receive any accrued interest. However, if they buy the bond after the coupon payment date, they will receive the accrued interest that has accumulated since the last payment.
Callable date
A callable date is a feature of some bonds that gives the issuer the option to redeem the bond before its maturity date. This can have a significant impact on how to calculate the zero coupon bond price.
If a bond is callable, the issuer has the right to redeem the bond at a specified price on or after the callable date. This means that the bondholder may not receive the full face value of the bond if the issuer exercises its call option. As a result, the price of a callable bond will be lower than the price of a non-callable bond with the same maturity and yield.
For example, let’s say that a company issues a $1,000 zero coupon bond with a maturity date of 10 years and a yield to maturity of 5%. The price of this bond would be $613.91. However, if the bond is callable in 5 years, the price would be lower because the issuer has the option to redeem the bond for $1,000 in 5 years.
Callable dates are an important consideration for investors when calculating the price of zero coupon bonds. Investors should be aware of the callable date and the call price before purchasing a bond. This information can be found in the bond’s prospectus.
Put date
A put date is a feature of some bonds that gives the bondholder the option to sell the bond back to the issuer at a specified price on or before a certain date. This can have a significant impact on how to calculate the zero coupon bond price.
- Definition
A put date is a contractual agreement between the bond issuer and the bondholder that gives the bondholder the right to sell the bond back to the issuer at a specified price on or before a certain date. - Impact on price
The put date can have a significant impact on the price of the bond. If the put date is close to the maturity date, the bond will trade at a price close to its face value. However, if the put date is far from the maturity date, the bond will trade at a discount to its face value. - Example
Let’s say that a company issues a $1,000 zero coupon bond with a maturity date of 10 years and a yield to maturity of 5%. If the bond has a put date of 5 years, the bond will trade at a price close to $1,000. However, if the bond has a put date of 1 year, the bond will trade at a discount to $1,000. - Considerations
When calculating the price of a zero coupon bond, it is important to consider the put date. The put date can have a significant impact on the bond’s price and yield to maturity.
Put dates are an important consideration for investors when calculating the price of zero coupon bonds. Investors should be aware of the put date and the put price before purchasing a bond. This information can be found in the bond’s prospectus.
FAQs on Zero Coupon Bond Calculations
This section addresses frequently asked questions and clarifies key aspects of calculating zero coupon bond prices.
Question 1: What is the formula for calculating the price of a zero coupon bond?
The price of a zero coupon bond is calculated as: Price = Face Value / (1 + Yield)^Time to Maturity.
Question 6: How does a callable date impact the bond price?
A callable date gives the issuer the option to redeem the bond before maturity. This lowers the bond’s price compared to a non-callable bond with the same maturity and yield.
These FAQs provide essential insights into the key factors and considerations involved in calculating zero coupon bond prices.
Next, we’ll delve deeper into practical examples to illustrate how these calculations are applied in real-world scenarios.
Tips for Calculating Zero Coupon Bond Prices
This section provides actionable tips to help you accurately calculate zero coupon bond prices:
Tip 1: Determine the Bond’s Face Value
Identify the face value, which represents the amount you’ll receive at maturity.
Tip 2: Establish the Bond’s Maturity Date
Pinpoint the maturity date to determine the bond’s time to maturity.
Tip 3: Calculate the Yield to Maturity
Estimate the annual rate of return you’ll earn by holding the bond until maturity.
Tip 4: Utilize the Zero Coupon Bond Pricing Formula
Apply the formula: Price = Face Value / (1 + Yield)^(Time to Maturity).
Tip 5: Consider Callable and Put Dates
Factor in callable and put dates, which can affect the bond’s price and yield.
Tip 6: Use a Financial Calculator or Spreadsheet
Simplify calculations using financial tools designed for bond pricing.
Tip 7: Consult Bond Market Data
Refer to reliable sources for up-to-date yield and price information.
Tip 8: Seek Professional Advice if Needed
Consider consulting a financial advisor for personalized guidance and complex calculations.
By following these tips, you’ll enhance the accuracy and efficiency of your zero coupon bond price calculations.
These calculations are crucial for making informed investment decisions, as they enable you to assess the potential return and risk associated with zero coupon bonds.
Conclusion
This comprehensive guide has delved into the intricacies of calculating zero coupon bond prices. We’ve explored the essential components involved in these calculations, including face value, maturity date, yield to maturity, and the impact of callable and put dates. By understanding these factors and applying the appropriate formulas, investors can accurately determine the price of zero coupon bonds.
Key takeaways include the significance of time to maturity, which inversely affects bond price, and the impact of interest rates on yield to maturity. Additionally, investors should carefully consider callable and put dates as they can influence the bond’s value and potential return.