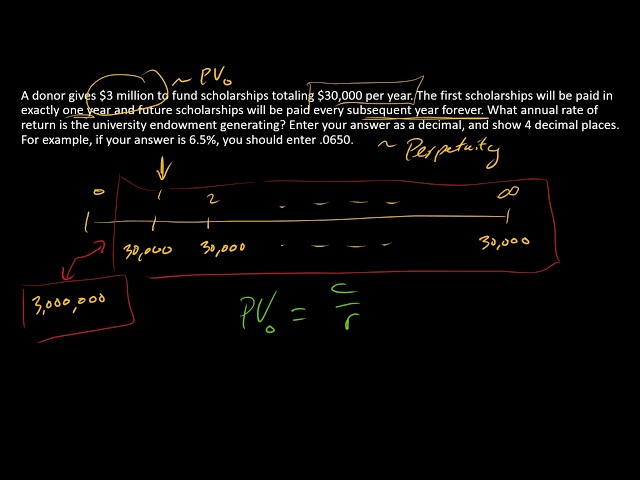
Calculating perpetuity discount rates, an essential financial concept, involves determining the discount rate used to value a stream of constant payments received indefinitely into the future.
This calculation plays a vital role in various financial domains, including bond valuation, project appraisal, and real estate investment. Understanding perpetuity discount rates empowers individuals and organizations to make informed decisions regarding long-term financial planning and asset valuation.
This article delves into the intricacies of perpetuity discount rate calculation, providing a comprehensive guide to its formula, applications, and practical implications for financial analysis and valuation.
How to Calculate Perpetuity Discount Rate
Understanding the essential aspects of perpetuity discount rate calculation is crucial for accurate financial analysis and valuation. These key aspects encompass various dimensions, including:
- Definition
- Formula
- Applications
- Assumptions
- Limitations
- Historical Context
- Impact of Interest Rates
- Relationship to Present Value
- Sensitivity Analysis
- Advanced Applications
These aspects provide a comprehensive framework for understanding perpetuity discount rates, their calculation, and their implications in financial decision-making. By delving into each aspect, individuals can gain a deeper appreciation of the nuances and complexities involved in perpetuity discount rate calculation.
Definition
In the context of perpetuity discount rate calculation, the definition serves as the cornerstone, providing the foundation for understanding the concept and its application. Without a clear definition, the calculation process becomes obscure and prone to misinterpretation.
The definition of perpetuity discount rate establishes its purpose and significance in financial analysis. It explains the concept of discounting future cash flows to determine the present value of an infinite stream of constant payments. This definition sets the stage for understanding the formula, assumptions, and limitations associated with perpetuity discount rate calculation.
In practical terms, the definition enables practitioners to apply the concept effectively. For instance, in bond valuation, the perpetuity discount rate represents the yield-to-maturity, which is crucial for determining the bond’s fair value. Similarly, in project appraisal, the perpetuity discount rate helps evaluate the long-term profitability of a project by considering the present value of its future cash flows.
Formula
The formula for calculating the perpetuity discount rate serves as the cornerstone of the calculation process, providing a mathematical framework for determining the discount rate used to value a stream of constant payments received indefinitely into the future. Without a well-defined formula, the calculation of perpetuity discount rates would be arbitrary and inconsistent, leading to inaccurate and unreliable results.
The formula establishes a clear relationship between the perpetuity discount rate (r) and the constant payment (C). It states that the perpetuity discount rate is equal to the constant payment divided by the present value of the perpetuity. This relationship highlights the inverse proportionality between the discount rate and the present value, implying that a higher discount rate results in a lower present value, and vice versa.
In practical applications, the perpetuity discount rate formula finds widespread use in various financial domains. For instance, in bond valuation, the formula helps determine the yield-to-maturity of a bond, which represents the annual rate of return an investor can expect to receive if they hold the bond until maturity. Similarly, in project appraisal, the formula assists in evaluating the long-term profitability of a project by considering the present value of its future cash flows.
Understanding the formula for calculating perpetuity discount rates is essential for accurate financial analysis and valuation. It provides a systematic approach to determining the discount rate, which is crucial for making informed decisions regarding long-term financial planning and asset valuation.
Applications
The applications of perpetuity discount rate calculation extend beyond theoretical concepts, finding practical use in diverse financial domains. These applications encompass various facets, each with its unique significance and implications.
- Bond Valuation
Perpetuity discount rate calculation plays a central role in bond valuation, determining the yield-to-maturity of a bond. This yield represents the annual rate of return an investor can expect if they hold the bond until maturity, making it crucial for informed investment decisions.
- Project Appraisal
In project appraisal, perpetuity discount rate calculation assists in evaluating the long-term profitability of a project. By considering the present value of its future cash flows, project managers can determine the project’s viability and make informed decisions regarding resource allocation.
- Real Estate Investment
Perpetuity discount rate calculation finds application in real estate investment, particularly in determining the value of properties that generate a constant stream of rental income. Investors use this calculation to assess the potential return on their investment and make informed purchasing decisions.
- Financial Planning
Perpetuity discount rate calculation is employed in financial planning to determine the present value of future financial obligations, such as pension payments or annuities. This calculation ensures that individuals and organizations can plan for their long-term financial security and make informed decisions regarding retirement savings and other financial goals.
These applications underscore the versatility and significance of perpetuity discount rate calculation in financial analysis and decision-making. By understanding the applications and implications of this calculation, individuals and organizations can make informed choices and navigate the complexities of long-term financial planning and asset valuation.
Assumptions
In the context of perpetuity discount rate calculation, assumptions play a crucial role in shaping the accuracy and applicability of the results. These assumptions provide the foundation upon which the calculation is based, and understanding their nature and implications is essential for informed decision-making.
- Constant Cash Flows
The perpetuity discount rate calculation assumes that the cash flows received indefinitely into the future are constant. This assumption simplifies the calculation process and aligns with the concept of a perpetuity, where payments remain unchanged over time.
- No Growth
The calculation further assumes that the cash flows do not experience any growth or inflation over time. This assumption implies that the purchasing power of the cash flows remains constant, which may not always hold true in real-world scenarios.
- Infinite Time Horizon
The perpetuity discount rate assumes an infinite time horizon, meaning that the cash flows continue indefinitely into the future. This assumption allows for the calculation of the present value of the entire stream of cash flows, but it may not be applicable in situations with finite time horizons.
- Risk-Free Environment
The calculation also assumes a risk-free environment, implying that there is no risk associated with receiving the cash flows. This assumption simplifies the calculation process but may not reflect the actual risk profile of the investment.
These assumptions provide a framework for perpetuity discount rate calculation, but it is important to recognize their limitations and apply them judiciously. By considering the potential impacts of these assumptions, practitioners can enhance the accuracy and reliability of their calculations and make more informed decisions.
Limitations
The calculation of perpetuity discount rates is subject to certain limitations, which can impact the accuracy and applicability of the results. Understanding these limitations is crucial for informed decision-making and effective financial analysis.
One key limitation is the assumption of constant cash flows. In reality, cash flows may fluctuate due to various factors, such as inflation, economic conditions, or changes in the underlying business. This assumption can lead to an oversimplified or inaccurate representation of the actual cash flow stream.
Another limitation lies in the assumption of no growth. Real-world cash flows often exhibit growth or decline over time due to factors such as inflation, technological advancements, or changes in market demand. Ignoring growth can result in an undervaluation or overvaluation of the perpetuity.
The practical implications of these limitations are significant. For example, in bond valuation, relying solely on perpetuity discount rate calculation without considering growth or inflation can lead to incorrect yield-to-maturity estimates. Similarly, in project appraisal, ignoring growth can result in an underestimation of the project’s long-term profitability.
Despite these limitations, perpetuity discount rate calculation remains a valuable tool for financial analysis and valuation. By understanding the limitations and applying the calculation judiciously, practitioners can enhance the accuracy of their results and make more informed decisions.
Historical Context
The historical context of how to calculate perpetuity discount rates provides valuable insights into the development and evolution of this financial concept. Understanding this context allows us to appreciate the reasons behind the formula and assumptions used in perpetuity discount rate calculations.
In the early days of finance, the concept of perpetuity was closely tied to the valuation of bonds and other fixed-income instruments. The need to determine the fair value of these investments led to the development of methods for calculating the present value of an infinite stream of constant payments. These methods formed the foundation for the modern formula used to calculate perpetuity discount rates.
Over time, the application of perpetuity discount rates expanded beyond bond valuation. Financial analysts recognized the usefulness of this concept in project appraisal, real estate investment, and other areas where long-term cash flows needed to be evaluated. As a result, the calculation of perpetuity discount rates became an integral part of financial analysis and decision-making.
In practical terms, understanding the historical context of perpetuity discount rate calculations helps practitioners appreciate the assumptions and limitations of this method. By recognizing the historical origins of the formula, analysts can better assess its applicability to different scenarios and make more informed decisions.
Impact of Interest Rates
The impact of interest rates plays a pivotal role in calculating perpetuity discount rates. Interest rates influence the present value of future cash flows, which is central to determining the perpetuity discount rate. Understanding this impact is crucial for accurate financial analysis and decision-making.
- Time Value of Money
Interest rates embody the time value of money, reflecting the concept that a sum of money today is worth more than the same sum in the future due to its earning potential. In calculating perpetuity discount rates, higher interest rates imply a lower present value for future cash flows, as the time value of money is more pronounced.
- Yield-to-Maturity
For bonds, the perpetuity discount rate is closely related to the yield-to-maturity, which is the effective annual rate of return an investor earns by holding the bond until maturity. Changes in interest rates directly impact the yield-to-maturity, which in turn affects the perpetuity discount rate used for bond valuation.
- Inflation
Interest rates are often viewed as a tool to combat inflation. Higher interest rates can help curb inflation by reducing demand and encouraging saving. In the context of perpetuity discount rate calculations, inflation can erode the real value of future cash flows, making it necessary to adjust the discount rate accordingly.
- Risk-Free Rate
The risk-free rate serves as a benchmark for determining perpetuity discount rates. It represents the rate of return on a hypothetical investment with no risk. Changes in the risk-free rate, often influenced by central bank policies, can have a significant impact on perpetuity discount rate calculations, especially for long-term investments.
In summary, the impact of interest rates on perpetuity discount rate calculations is multifaceted. It encompasses the time value of money, yield-to-maturity, inflation, and the risk-free rate. Understanding these factors enables practitioners to make informed decisions and conduct accurate financial analysis, particularly when valuing long-term investments and assessing the present value of future cash flows.
Relationship to Present Value
The intimate relationship between how to calculate perpetuity discount rate and present value underpins the valuation of long-term financial instruments and assets. Present value represents the current worth of a future sum of money, discounted at a specified rate. Understanding this relationship allows for accurate financial planning and investment decision-making.
- Time Value of Money
Present value acknowledges the time value of money, recognizing that a dollar today is worth more than a dollar in the future due to its earning potential. Perpetuity discount rate calculation incorporates this concept by discounting future cash flows to determine their present value.
- Valuation of Perpetuities
Perpetuities, representing an infinite stream of constant payments, are valued using perpetuity discount rates. The discount rate effectively translates the future cash flows into a single present value, providing insights into the current worth of the perpetuity.
- Bond Pricing
In bond pricing, the perpetuity discount rate is closely tied to the yield-to-maturity. By discounting the future coupon payments and the principal repayment at maturity, the present value of the bond can be determined, influencing its market price.
- Project Appraisal
Perpetuity discount rates play a crucial role in project appraisal, particularly when assessing long-term projects with an indefinite lifespan. By considering the present value of future cash flows, project managers can evaluate the viability and profitability of investment opportunities.
In summary, the relationship between how to calculate perpetuity discount rate and present value forms the cornerstone of valuing long-term financial instruments and assets. It considers the time value of money, enables the valuation of perpetuities, assists in bond pricing, and supports project appraisal. Understanding this relationship is essential for informed financial decision-making and effective financial planning.
Sensitivity Analysis
Sensitivity analysis is a crucial component of calculating perpetuity discount rates, enabling us to assess the impact of changing input variables on the final result. By examining potential variations and their effects, we gain a deeper understanding of the robustness and reliability of our calculations.
- Impact of Discount Rate
Altering the discount rate used can significantly affect the perpetuity discount rate, highlighting the sensitivity of the calculation to this input variable. Changes in the discount rate can lead to substantial variations in the present value of future cash flows.
- Duration and Cash Flow Variability
The duration and variability of cash flows also influence the perpetuity discount rate. Longer durations and higher variability can result in more pronounced changes in the discount rate, emphasizing the importance of considering these factors in the analysis.
- Growth Assumptions
Assumptions regarding the growth rate of cash flows can impact the perpetuity discount rate. Sensitivity analysis allows us to explore different growth scenarios and their effects on the final result, providing insights into the potential impact of growth on the valuation.
- Real-World Applications
Sensitivity analysis finds practical applications in project appraisal, bond pricing, and other financial decision-making contexts. By understanding how changes in input variables affect perpetuity discount rates, analysts can make more informed and robust recommendations.
In conclusion, sensitivity analysis is an essential tool in perpetuity discount rate calculation, allowing us to gauge the sensitivity of the result to various input variables. By incorporating sensitivity analysis into our calculations, we enhance the reliability and accuracy of our financial analysis and decision-making processes.
Advanced Applications
Advanced applications of perpetuity discount rate calculation extend beyond basic valuation techniques, opening up a realm of sophisticated financial analysis and decision-making. These applications leverage the core principles of perpetuity discount rates while incorporating additional complexities and real-world considerations.
- Stochastic Discount Factors
Incorporating stochasticity into perpetuity discount rate calculations allows for modeling uncertainty in future cash flows. This approach captures the potential variability of cash flows, resulting in more realistic and robust valuations.
- Option-Adjusted Discount Rates
When valuing assets with embedded options, such as convertible bonds or real estate with development potential, option-adjusted discount rates are employed. These rates adjust for the optionality embedded in the asset, providing a more accurate reflection of its value.
- Contingent Claims Valuation
Perpetuity discount rates play a crucial role in valuing contingent claims, such as insurance policies or derivatives. By considering the potential outcomes and probabilities associated with these claims, analysts can determine their fair value.
- Real Estate Investment Trusts (REITs)
In real estate investment trusts (REITs), perpetuity discount rates are used to value the underlying portfolio of properties. This approach considers the long-term income-generating potential of the properties, providing investors with insights into the REIT’s overall value.
These advanced applications underscore the versatility and power of perpetuity discount rate calculation. By incorporating sophisticated techniques and real-world considerations, financial analysts can enhance the accuracy and reliability of their valuations, make more informed decisions, and navigate the complexities of modern financial markets.
Frequently Asked Questions on Calculating Perpetuity Discount Rates
This section addresses common queries and clarifies aspects related to calculating perpetuity discount rates, providing concise and informative answers.
Question 1: What is the significance of perpetuity discount rates in financial analysis?
Answer: Perpetuity discount rates play a crucial role in valuing long-term investments, such as bonds, real estate, and projects with indefinite lifespans. They help determine the present value of an infinite stream of constant payments, providing insights into the asset’s or project’s worth.
Question 2: How do I calculate the perpetuity discount rate?
Answer: The perpetuity discount rate is calculated by dividing the constant payment by the present value of the perpetuity. The present value is determined using the formula PV = C / r, where C represents the constant payment and r represents the perpetuity discount rate.
Question 3: What are the key assumptions in perpetuity discount rate calculations?
Answer: Perpetuity discount rate calculations assume constant cash flows, no growth, an infinite time horizon, and a risk-free environment. These assumptions simplify the calculation but may not always align with real-world scenarios.
Question 6: How do interest rates impact perpetuity discount rates?
Answer: Interest rates have a significant impact on perpetuity discount rates. Higher interest rates result in lower present values of future cash flows, leading to higher perpetuity discount rates. Conversely, lower interest rates result in higher present values and lower perpetuity discount rates.
Summary: These FAQs provide essential insights into calculating perpetuity discount rates, highlighting their significance, formula, assumptions, and the impact of interest rates. Understanding these concepts is crucial for accurate financial analysis and informed decision-making.
Transition: In the next section, we will delve into advanced applications of perpetuity discount rates, exploring techniques such as stochastic discount factors and option-adjusted discount rates, to enhance the accuracy and sophistication of financial valuations.
Tips for Calculating Perpetuity Discount Rates
This section provides practical tips to enhance the accuracy and effectiveness of perpetuity discount rate calculations, ensuring informed financial analysis and decision-making.
Tip 1: Carefully consider the assumptions underlying perpetuity discount rate calculations, such as constant cash flows and no growth. Assess their applicability to the specific scenario and make adjustments as necessary.
Tip 2: Utilize sensitivity analysis to gauge the impact of changing input variables, such as discount rate and cash flow assumptions, on the perpetuity discount rate. This analysis provides insights into the robustness of the calculation.
Tip 3: When dealing with variable or uncertain cash flows, consider employing stochastic discount factors to capture the potential variability and enhance the reliability of the calculation.
Tip 4: For assets with embedded options, such as convertible bonds, incorporate option-adjusted discount rates to account for the optionality and provide a more accurate valuation.
Tip 5: In real estate investment trusts (REITs), use perpetuity discount rates to assess the long-term income-generating potential of the underlying properties and determine the REIT’s overall value.
By incorporating these tips into perpetuity discount rate calculations, financial analysts can improve the accuracy and reliability of their valuations, make informed decisions, and navigate the complexities of modern financial markets.
The following section concludes our discussion on calculating perpetuity discount rates, summarizing the key takeaways and emphasizing their importance in various financial applications.
Conclusion
This comprehensive exploration of calculating perpetuity discount rates has illuminated the significance of this concept in financial analysis and valuation. We have examined the definition, formula, assumptions, and limitations of perpetuity discount rates, gaining a deeper understanding of their role in assessing the present value of long-term cash flows.
Key takeaways from our discussion include the inverse relationship between perpetuity discount rates and present value, the importance of considering assumptions and limitations in practical applications, and the impact of interest rates on the calculation. These interconnected concepts provide a solid foundation for calculating perpetuity discount rates and utilizing them effectively in various financial contexts.