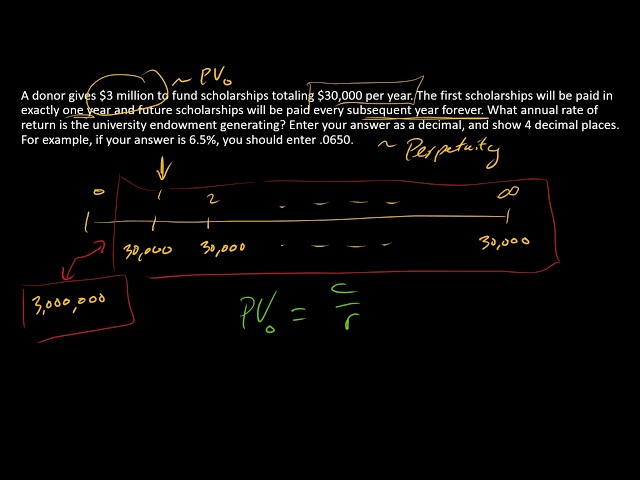
Calculating a discount rate for perpetuity assesses the present value of an infinite stream of income. For example, a utility company might project cash flows over the next century or beyond.
This technique is vital for financial planning, investment decisions, and determining the value of long-term assets. Historically, the development of discounted cash flow analysis in the 1950s provided a framework for calculating the present value of future cash flows.
This article delves into the methods and considerations involved in calculating discount rates for perpetuity, equipping readers with the knowledge to analyze and evaluate future income streams accurately.
How to Calculate Discount Rate for Perpetuity
Determining the discount rate for perpetuity is essential for accurately assessing the present value of an infinite stream of income. Here are 10 key aspects to consider when calculating the discount rate for perpetuity:
- Risk-free rate
- Inflation rate
- Equity risk premium
- Maturity risk premium
- Company-specific risk
- Terminal growth rate
- Tax rate
- Horizon
- Sensitivity
- Assumptions
These aspects are interconnected and should be carefully considered to ensure an accurate discount rate calculation. For example, the risk-free rate represents the return on a risk-free investment, while the equity risk premium compensates for the additional risk associated with investing in stocks. The terminal growth rate assumes a constant growth rate for the perpetuity beyond the explicit forecast period. Sensitivity analysis can assess the impact of changes in key assumptions on the discount rate. Understanding these key aspects is crucial for calculating an appropriate discount rate for perpetuity, which is essential for making informed investment decisions.
Risk-free rate
The risk-free rate plays a fundamental role in determining the discount rate for perpetuity. It represents the rate of return on an investment with no risk, such as a government bond. In the context of calculating the discount rate for perpetuity, the risk-free rate serves as the starting point for building up the required rate of return. This is because investors typically demand a higher return for taking on more risk, and the discount rate for perpetuity must reflect this risk premium.
For example, if the risk-free rate is 2% and the equity risk premium is 5%, then the discount rate for perpetuity for a stock would be 7%. This means that investors would require a 7% return on their investment in the stock to compensate for the additional risk they are taking compared to investing in a risk-free government bond.
The risk-free rate is a critical component of calculating the discount rate for perpetuity because it provides a benchmark against which the risk premium can be assessed. Without a risk-free rate, it would be difficult to determine an appropriate discount rate that reflects the time value of money and the level of risk associated with the investment.
Inflation rate
In the context of calculating the discount rate for perpetuity, the inflation rate plays a crucial role in determining the real return on investment. Inflation erodes the purchasing power of money over time, which means that a dollar today is worth less than a dollar in the future. Therefore, investors must account for inflation when calculating the discount rate to ensure that they are receiving a real return on their investment.
- Expected inflation rate
The expected inflation rate is the rate at which inflation is forecast to increase over the life of the investment. It is a key component in calculating the discount rate because it affects the real return on investment.
- Historical inflation rate
The historical inflation rate is the average rate of inflation over a specific period in the past. It can be used to estimate the expected inflation rate, although it is not a guarantee of future inflation rates.
- Inflation risk premium
The inflation risk premium is the additional return that investors demand to compensate for the risk of inflation eroding the value of their investment. It is typically added to the real risk-free rate to determine the nominal discount rate.
- Impact on discount rate
The inflation rate has a direct impact on the discount rate. A higher inflation rate will result in a higher discount rate, which in turn will lower the present value of future cash flows.
In conclusion, understanding the inflation rate and its components is essential for accurately calculating the discount rate for perpetuity. By considering the expected inflation rate, historical inflation rate, inflation risk premium, and the impact on the discount rate, investors can make informed decisions about the appropriate discount rate to use for their investments.
Equity risk premium
Equity risk premium (ERP) plays a pivotal role in calculating the discount rate for perpetuity. It compensates investors for the additional risk associated with investing in stocks compared to risk-free investments. Several facets contribute to ERP:
- Market risk premium
This is the difference between the expected return on the stock market and the risk-free rate. It reflects the overall riskiness of the stock market and is influenced by factors such as economic conditions, interest rates, and political stability.
- Company-specific risk premium
This is the additional risk associated with investing in a particular company. It is influenced by factors such as the company’s financial health, industry outlook, and management team.
- Liquidity risk premium
This is the premium investors demand for investing in less liquid stocks. Less liquid stocks are more difficult to buy and sell, which can lead to losses if investors need to sell quickly.
- Inflation risk premium
This is the premium investors demand to compensate for the risk that inflation will erode the value of their investment. Inflation can reduce the real return on investment, so investors demand a higher return to offset this risk.
Understanding these facets of equity risk premium is crucial for accurately calculating the discount rate for perpetuity. ERP is an essential component of the discount rate, and considering its various components ensures that the discount rate reflects the true riskiness of the investment.
Maturity risk premium
Maturity risk premium (MRP) is a critical component of calculating the discount rate for perpetuity. It reflects the additional return that investors demand for taking on the risk of investing in longer-term bonds. This is because longer-term bonds are subject to greater interest rate risk than shorter-term bonds. Interest rate risk is the risk that the value of a bond will decline if interest rates rise. The longer the maturity of a bond, the greater the interest rate risk.
MRP is typically calculated as the difference between the yield on a long-term bond and the yield on a short-term bond. For example, if the yield on a 10-year Treasury bond is 3% and the yield on a 2-year Treasury bond is 2%, then the MRP would be 1%. This means that investors would demand a 1% higher return for investing in the 10-year bond compared to the 2-year bond.
MRP is an important consideration when calculating the discount rate for perpetuity because it affects the present value of future cash flows. A higher MRP will result in a lower present value, while a lower MRP will result in a higher present value. This is because a higher MRP implies that investors demand a higher return for taking on the risk of investing in longer-term cash flows.
Company-specific risk
Company-specific risk is a crucial factor in calculating the discount rate for perpetuity. It captures the unique risks associated with a particular company, which can significantly affect the value of its future cash flows. Understanding and quantifying company-specific risk is essential for determining an appropriate discount rate that reflects the true riskiness of the investment.
Company-specific risk arises from various factors, including the company’s financial health, industry outlook, competitive landscape, and management team. For example, a company with a high level of debt may have a higher risk of default, which would reduce the value of its future cash flows. Similarly, a company operating in a highly competitive industry may face greater uncertainty in its future earnings, leading to a higher discount rate.
Real-life examples of company-specific risk include the impact of the COVID-19 pandemic on the airline industry, the fluctuations in oil prices on energy companies, and the effects of technological disruption on traditional businesses. These events highlight the importance of considering company-specific risk when calculating the discount rate for perpetuity, as they can significantly alter the present value of future cash flows.
Practically, understanding the connection between company-specific risk and the discount rate for perpetuity allows investors to make more informed investment decisions. By incorporating company-specific risk into their analysis, investors can better assess the potential risks and rewards of an investment and determine an appropriate discount rate that reflects their risk tolerance and investment goals.
Terminal growth rate
Terminal growth rate plays a crucial role in calculating the discount rate for perpetuity. It represents the constant growth rate assumed for the perpetuity beyond the explicit forecast period. By incorporating a terminal growth rate, investors can account for the assumption that the perpetuity’s cash flows will not remain constant indefinitely.
The terminal growth rate is often estimated using various methods, such as the Gordon growth model or industry analysis. It should be aligned with the expected long-term growth rate of the economy, industry, or specific company being evaluated. In practice, the terminal growth rate is typically lower than the historical growth rate, reflecting the belief that growth rates tend to slow down over time.
Understanding the connection between terminal growth rate and the discount rate for perpetuity is essential for accurate valuation. A higher terminal growth rate leads to a higher discount rate, which in turn results in a lower present value of the perpetuity. Conversely, a lower terminal growth rate implies a lower discount rate and a higher present value. This relationship highlights the importance of carefully considering the appropriate terminal growth rate to ensure a reasonable and reliable valuation.
Tax rate
Tax rate is an influential factor in the calculation of the discount rate for perpetuity. It affects the after-tax cash flows that investors receive, which in turn impacts the present value of the perpetuity. Understanding the relationship between tax rate and the discount rate for perpetuity is crucial for accurate valuation and investment decision-making.
Tax rate directly affects the calculation of the discount rate through its impact on the after-tax cost of debt. The after-tax cost of debt is the cost of borrowing after considering the tax savings from interest payments. A higher tax rate leads to a lower after-tax cost of debt, which in turn reduces the discount rate. Conversely, a lower tax rate results in a higher after-tax cost of debt and a higher discount rate.
Real-life examples of the impact of tax rate on the discount rate for perpetuity can be observed in the analysis of companies operating in different tax jurisdictions. For instance, a company operating in a country with a high corporate tax rate would have a higher discount rate compared to a similar company operating in a country with a lower tax rate. This is because the higher tax rate reduces the after-tax cash flows and, consequently, the present value of the perpetuity.
The practical significance of understanding the connection between tax rate and the discount rate for perpetuity lies in its implications for investment decisions. Investors need to consider the tax implications of their investments and adjust the discount rate accordingly to arrive at a more accurate valuation. Failure to account for tax rates can lead to incorrect investment decisions and potential losses.
Horizon
Horizon, in the context of calculating the discount rate for perpetuity, refers to the period over which the perpetuity is expected to generate cash flows. It plays a critical role in determining the present value of the perpetuity, as the discount rate is applied over the horizon period to discount future cash flows back to the present.
- Explicit Forecast Period
This is the finite period for which explicit cash flow projections are available. It is typically several years, such as 5 or 10 years.
- Terminal Value
This is the value of the perpetuity beyond the explicit forecast period. It is calculated using a terminal growth rate, which assumes a constant growth rate for the perpetuity in perpetuity.
- Perpetuity Period
This is the infinite period beyond the terminal value. It assumes that the perpetuity will continue to generate cash flows indefinitely at the terminal growth rate.
Understanding the concept of horizon is crucial for accurately calculating the discount rate for perpetuity. The explicit forecast period provides a basis for estimating near-term cash flows, while the terminal value and perpetuity period account for the long-term cash flows. By considering the entire horizon, investors can make informed decisions about the appropriate discount rate to use, ensuring a reliable valuation of the perpetuity.
Sensitivity
In the context of calculating the discount rate for perpetuity, sensitivity analysis plays a crucial role in assessing the robustness and reliability of the calculated discount rate. Sensitivity analysis involves testing how the discount rate changes in response to changes in the underlying assumptions and parameters.
- Risk Parameters
Sensitivity analysis can be performed on various risk parameters, such as the risk-free rate, equity risk premium, and maturity risk premium. By varying these parameters within reasonable ranges, investors can observe the impact on the discount rate and the resulting present value of the perpetuity.
- Growth Rate
The terminal growth rate is a key assumption in perpetuity calculations. Sensitivity analysis can be used to test the impact of different growth rates on the discount rate. This is particularly important when there is uncertainty about the long-term growth prospects of the underlying asset or business.
- Horizon
The horizon, or the period over which the perpetuity is expected to generate cash flows, can also be subject to sensitivity analysis. By varying the horizon, investors can assess how the discount rate and present value change based on different assumptions about the duration of the cash flows.
- Tax Rate
The tax rate can significantly impact the discount rate, especially for companies operating in different tax jurisdictions. Sensitivity analysis can help investors understand how changes in the tax rate affect the discount rate and the present value of the perpetuity.
Sensitivity analysis provides valuable insights into the sensitivity of the discount rate to changes in key assumptions. By conducting sensitivity analysis, investors can make more informed decisions about the appropriate discount rate to use, mitigate potential risks, and increase the reliability of their perpetuity calculations.
Assumptions
Assumptions play a critical role in the calculation of the discount rate for perpetuity. The discount rate is used to determine the present value of an infinite stream of future cash flows, and the accuracy of this calculation relies heavily on the validity of the assumptions made. These assumptions include the risk-free rate, equity risk premium, terminal growth rate, and horizon period. Any changes in these assumptions can significantly impact the calculated discount rate and, consequently, the present value of the perpetuity.
For instance, a higher risk-free rate implies a higher cost of borrowing, which in turn leads to a higher discount rate. This higher discount rate would result in a lower present value for the perpetuity. Similarly, a higher terminal growth rate suggests that the perpetuity’s cash flows are expected to grow at a faster rate in the future, which would lead to a higher present value.
In practice, understanding the connection between assumptions and the discount rate for perpetuity is essential for making informed investment decisions. Investors need to carefully consider the reasonableness of the assumptions used in the calculation and assess the potential impact of changes in these assumptions on the present value of the perpetuity. This understanding enables investors to make more accurate valuations and mitigate potential risks.
Frequently Asked Questions
This section addresses common questions and clarifies concepts related to calculating the discount rate for perpetuity.
Question 1: What is the purpose of calculating the discount rate for perpetuity?
Answer: The discount rate for perpetuity helps determine the present value of an infinite stream of future cash flows, which is essential for evaluating long-term investments and financial planning.
Question 2: What are the key factors that influence the discount rate for perpetuity?
Answer: The discount rate is influenced by the risk-free rate, equity risk premium, terminal growth rate, horizon period, and tax rate.
Question 3: How do I determine the appropriate risk-free rate for perpetuity calculations?
Answer: The risk-free rate is typically based on government bonds with maturities similar to the horizon of the perpetuity.
Question 4: What is the role of the terminal growth rate in calculating the discount rate for perpetuity?
Answer: The terminal growth rate represents the constant growth rate assumed for the perpetuity beyond the explicit forecast period.
Question 5: How does the horizon period impact the discount rate for perpetuity?
Answer: The horizon period, or the duration of the perpetuity’s cash flows, affects the number of cash flows discounted and can influence the present value.
Question 6: What are some common mistakes to avoid when calculating the discount rate for perpetuity?
Answer: Common mistakes include using an inappropriate risk-free rate, neglecting the terminal growth rate, and not considering the impact of taxes.
These FAQs provide essential insights into calculating the discount rate for perpetuity. Understanding these concepts is crucial for accurate financial planning and investment decision-making.
In the next section, we will explore practical applications of the discount rate for perpetuity in various financial scenarios.
Tips for Calculating the Discount Rate for Perpetuity
To ensure accurate and reliable calculations of the discount rate for perpetuity, it is essential to follow certain best practices and consider the following actionable tips:
Tip 1: Use a reasonable risk-free rate. Consider government bonds with maturities similar to the horizon of the perpetuity.
Tip 2: Determine an appropriate equity risk premium based on market conditions, company-specific factors, and the level of risk aversion.
Tip 3: Estimate a realistic terminal growth rate that aligns with industry expectations and the long-term economic outlook.
Tip 4: Carefully select the horizon period, considering the expected duration of the perpetuity’s cash flows and the level of uncertainty involved.
Tip 5: Factor in the impact of taxes, as they can significantly affect the after-tax cost of debt and, consequently, the discount rate.
Tip 6: Conduct sensitivity analysis to assess the impact of changes in key assumptions on the discount rate and present value.
Tip 7: Use appropriate financial models and tools to perform the calculations accurately and efficiently.
Tip 8: Regularly review and update the discount rate as market conditions and assumptions change over time.
By adhering to these tips, you can enhance the accuracy and reliability of your discount rate calculations for perpetuity, leading to more informed investment decisions and financial planning.
In the following section, we will delve into the practical applications of the discount rate for perpetuity in various financial scenarios, demonstrating its significance in financial analysis and decision-making.
Conclusion
In summary, calculating the discount rate for perpetuity involves a comprehensive analysis of various factors, including the risk-free rate, equity risk premium, terminal growth rate, horizon period, and tax rate. Understanding the interconnections between these factors is crucial for determining an appropriate discount rate that accurately reflects the risk and expected returns of the underlying perpetuity.
Key takeaways include the importance of using reasonable assumptions, conducting sensitivity analysis, and regularly reviewing and updating the discount rate. By adhering to best practices and leveraging appropriate financial models, investors can increase the accuracy and reliability of their perpetuity calculations.
Calculating the discount rate for perpetuity remains a fundamental aspect of financial analysis and decision-making, enabling investors to evaluate long-term investments, plan for the future, and make informed choices in uncertain markets.