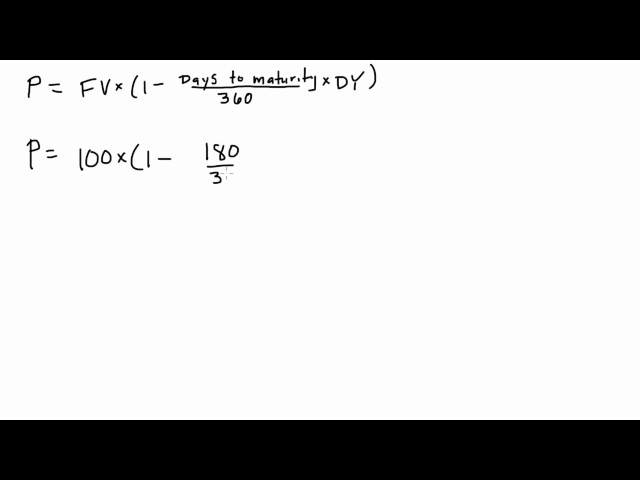The discount rate to yield formula is a mathematical equation that calculates the yield-to-maturity of a fixed income security, such as a bond or a loan.
It is a crucial concept in finance, as it helps investors and analysts determine the potential return on their investments.
This article will explore the discount rate to yield formula in detail, providing insights into its significance, advantages, and historical evolution. We will also discuss practical applications and limitations of the formula.
discount rate to yield formula
The discount rate to yield formula is a vital tool in fixed income investing, as it helps investors calculate the potential return on their investments. Key aspects of the discount rate to yield formula include:
- Definition
- Formula
- Assumptions
- Limitations
- Applications
- Historical context
- Advantages
- Disadvantages
These aspects provide a comprehensive understanding of the discount rate to yield formula, its usage, and its significance in the financial markets. By understanding these aspects, investors can effectively evaluate fixed income securities and make informed investment decisions.
Definition
In the context of the discount rate to yield formula, “Definition” refers to the precise mathematical equation used to calculate the yield-to-maturity of a fixed income security. This equation is crucial for determining the potential return on an investment in such securities.
The discount rate to yield formula is a critical component of fixed income investing, as it provides investors with a standardized method for evaluating and comparing different securities. By utilizing this formula, investors can make informed decisions about which investments align with their financial goals and risk tolerance.
A practical application of this understanding is in the valuation of bonds. The discount rate to yield formula is used to determine the present value of future cash flows associated with a bond, which is essential for assessing its fair market value. This information is vital for both individual investors and financial institutions when making investment decisions.
In summary, the “Definition” of the discount rate to yield formula is of utmost importance, as it provides the foundation for calculating the yield-to-maturity of fixed income securities. This understanding enables investors to make informed investment decisions and accurately value bonds.
Formula
The “Formula” in the context of the discount rate to yield formula refers to the mathematical equation used to calculate the yield-to-maturity of a fixed income security. This formula is of paramount importance as it enables investors to determine the potential return on their investments.
- Components
The formula consists of several components, including the present value of the future cash flows, the face value of the security, and the number of periods until maturity. - Variables
The formula involves variables such as the discount rate, which represents the rate of return an investor expects to earn on the investment. - Real-Life Application
The formula is used in practice to calculate the yield-to-maturity of bonds, which is a key factor in determining their fair market value. - Implications
The formula’s implications extend to financial analysis, portfolio management, and risk assessment in fixed income markets.
In summary, the “Formula” in the context of the discount rate to yield formula is a mathematical equation that plays a crucial role in evaluating fixed income securities. Its components, variables, real-life applications, and implications highlight its significance in the financial markets.
Assumptions
In the context of the discount rate to yield formula, “Assumptions” refer to the underlying conditions and expectations that are incorporated into the formula’s calculations. These assumptions play a critical role in determining the accuracy and applicability of the formula in real-life scenarios.
- Constant Interest Rates
The formula assumes that interest rates will remain constant throughout the life of the security. This assumption simplifies the calculation process but may not always reflect the dynamic nature of financial markets. - Regular Cash Flows
The formula assumes that the security will make regular and predictable cash flows, such as coupon payments or principal repayments. This assumption may not hold true for all types of fixed income securities or in cases of default. - Default Risk
The formula typically does not incorporate default risk, which is the possibility that the issuer of the security may fail to make timely payments or repay the principal. This assumption can lead to an underestimation of the actual yield. - Tax Implications
The formula does not account for the potential impact of taxes on the yield. Tax laws and regulations can vary, and their effects on the net return should be considered separately.
These assumptions provide a simplified framework for calculating yield-to-maturity, but it is important to recognize their limitations and potential impact on the accuracy of the results. Practitioners should carefully evaluate the underlying assumptions and make necessary adjustments to ensure a more realistic assessment of fixed income investments.
Limitations
The limitations of the discount rate to yield formula stem from the assumptions it employs to simplify calculations. These assumptions can lead to deviations from real-world scenarios, potentially affecting the accuracy of the yield-to-maturity calculations.
One significant limitation is the assumption of constant interest rates. In practice, interest rates fluctuate over time, and this can impact the actual yield-to-maturity. As a result, the formula may provide an overly simplistic view of the potential return on investment.
Another limitation is the assumption of regular and predictable cash flows. In reality, there is always a risk of default or late payments, which can significantly alter the actual yield. The formula does not account for such risks, potentially leading to an underestimation of the true yield.
Despite these limitations, the discount rate to yield formula remains a valuable tool for fixed income analysis. By understanding the assumptions and limitations, practitioners can use the formula more effectively and make more informed investment decisions. It is critical to consider the potential impact of these limitations and adjust the analysis accordingly to enhance the accuracy of yield-to-maturity calculations.
Applications
The applications of the discount rate to yield formula extend beyond theoretical calculations. It is widely used in various financial practices and investment strategies, providing valuable insights for decision-making.
- Bond Pricing
The formula is central to bond pricing, enabling investors to determine the fair market value of bonds based on their yield-to-maturity and other factors.
- Portfolio Management
The formula assists portfolio managers in constructing and managing fixed income portfolios, helping them optimize yield and minimize risk.
- Risk Assessment
By incorporating the discount rate into risk assessment models, analysts can evaluate the potential impact of interest rate fluctuations on fixed income investments.
- Investment Analysis
The formula is a key tool for investment analysts, allowing them to compare the yields of different fixed income securities and make informed investment recommendations.
In summary, the applications of the discount rate to yield formula are diverse and crucial in the fixed income markets. From bond pricing to portfolio management and risk assessment, this formula provides a solid foundation for informed decision-making and effective investment strategies.
Historical context
The historical context plays a crucial role in understanding the development and evolution of the discount rate to yield formula. This formula is deeply rooted in the history of financial markets and has undergone significant changes and refinements to meet the evolving needs of investors and analysts.
The concept of discounting future cash flows to determine their present value has been used for centuries. However, the formalization of the discount rate to yield formula is attributed to the work of mathematicians and economists in the 18th and 19th centuries. Notably, the development of bond pricing models and the need for accurate yield calculations contributed to the refinement of the formula.
Historical events, such as economic crises and periods of high inflation, have also influenced the development of the discount rate to yield formula. For instance, the Great Depression led to a reassessment of the assumptions underlying the formula and the recognition of the importance of incorporating risk and uncertainty into yield calculations.
Understanding the historical context of the discount rate to yield formula provides valuable insights into its strengths, limitations, and practical applications. By examining how the formula has evolved over time, investors and analysts can gain a deeper appreciation of its significance in fixed income markets and make more informed decisions.
Advantages
The discount rate to yield formula offers numerous advantages that make it a valuable tool for investors and analysts in fixed income markets.
- Accurate Yield Calculations
The formula provides accurate yield-to-maturity calculations, allowing investors to determine the true potential return on their fixed income investments, taking into account the time value of money and the present value of future cash flows.
- Objective and Standardized
The formula is objective and standardized, providing a consistent method for calculating yield-to-maturity across different fixed income securities. This enables investors to compare yields and make informed decisions based on objective data.
- Transparency and Simplicity
The formula is relatively simple to understand and apply, making it accessible to a wide range of users, including individual investors and financial professionals. Its transparency allows users to verify and replicate yield calculations, enhancing trust in the results.
- Wide Applicability
The formula is widely applicable to a variety of fixed income securities, including bonds, notes, and other debt instruments. This versatility makes it a useful tool for analyzing and valuing fixed income portfolios and making investment decisions.
In summary, the advantages of the discount rate to yield formula lie in its accuracy, objectivity, simplicity, and wide applicability. These advantages make it an essential tool for investors and analysts seeking to make informed decisions in fixed income markets.
Disadvantages
While the discount rate to yield formula offers numerous advantages, there are certain disadvantages to consider that may limit its applicability in certain situations or introduce potential inaccuracies.
- Simplicity Assumption
The formula assumes that future cash flows and interest rates remain constant, which may not always hold true in real-world scenarios. This assumption can lead to yield calculations that deviate from actual market conditions.
- Default Risk
The formula does not explicitly incorporate default risk, which poses a challenge when evaluating fixed income securities issued by entities with varying creditworthiness. Ignoring default risk can result in overstated yield estimates.
- Tax Considerations
The formula does not account for the impact of taxes on the yield-to-maturity. Tax laws and regulations can vary, affecting the net return on fixed income investments. This can lead to discrepancies between the calculated yield and the actual after-tax return.
- Market Volatility
The formula assumes that interest rates and market conditions remain stable over the life of the security, which may not always be the case. Significant market fluctuations can lead to substantial deviations between the calculated yield and the actual yield realized in practice.
Overall, while the discount rate to yield formula provides a valuable framework for yield calculations, it is important to recognize its limitations and potential drawbacks. By considering these disadvantages and adjusting the analysis accordingly, investors and analysts can enhance the accuracy of their yield estimates and make more informed investment decisions.
Frequently Asked Questions
This section addresses some of the most common questions and concerns regarding the discount rate to yield formula. These FAQs aim to clarify key concepts, address potential misconceptions, and provide additional insights for better understanding and application of the formula.
Question 1: What is the purpose of the discount rate to yield formula?
Answer: The discount rate to yield formula is used to calculate the yield-to-maturity of a fixed income security, which represents the annual rate of return an investor can expect to earn if they hold the security until its maturity date.
Question 2: What are the key assumptions of the discount rate to yield formula?
Answer: The formula assumes that future cash flows and interest rates remain constant over the life of the security. It also assumes that the security will not default and that taxes do not affect the yield-to-maturity.
Question 6: What are the limitations of the discount rate to yield formula?
Answer: The formula’s limitations include its sensitivity to changes in interest rates, its lack of consideration for default risk, and its inability to account for the impact of taxes on the yield-to-maturity.
In summary, these FAQs have provided insights into the purpose, assumptions, advantages, and limitations of the discount rate to yield formula. By understanding these aspects, investors and analysts can effectively utilize the formula for accurate yield calculations and informed investment decisions. As we delve deeper into the discussion, the next section will explore advanced applications and extensions of the formula, enabling a comprehensive understanding of its role in fixed income analysis.
Transition to the next article section: Advanced Applications of the Discount Rate to Yield Formula
TIPS for Understanding and Applying the Discount Rate to Yield Formula
This section provides practical tips for effectively understanding and applying the discount rate to yield formula in fixed income analysis.
Tip 1: Grasp the Underlying Concepts
Thoroughly understand the concepts of present value, future value, and the time value of money to build a solid foundation for applying the formula.
Tip 2: Identify the Formula’s Components
Familiarize yourself with the formula’s components, including the face value, coupon payments, number of periods, and discount rate, to ensure accurate calculations.
Tip 6: Consider Default Risk
While the formula typically does not incorporate default risk, be aware of the potential for default and adjust your analysis accordingly to account for this risk.
Tip 7: Explore Advanced Applications
Extend your knowledge beyond basic calculations by exploring advanced applications of the formula, such as calculating yield-to-call and yield-to-worst.
Summary:By following these tips, you can enhance your understanding and application of the discount rate to yield formula, enabling more accurate yield calculations and informed fixed income investment decisions.
Transition:In the concluding section, we will summarize the key points discussed throughout the article and emphasize the importance of understanding and using the discount rate to yield formula effectively in fixed income analysis.
Conclusion
In summary, the discount rate to yield formula is a critical tool for fixed income analysis, enabling investors to calculate the yield-to-maturity of fixed income securities. Understanding the formula’s components, assumptions, advantages, and limitations is essential for accurate yield calculations and informed investment decisions.
Key takeaways include the formula’s reliance on assumptions that may not always hold true in practice, the need to consider default risk, and the formula’s sensitivity to changes in interest rates. Advanced applications of the formula extend beyond basic yield calculations, providing valuable insights for fixed income investors.