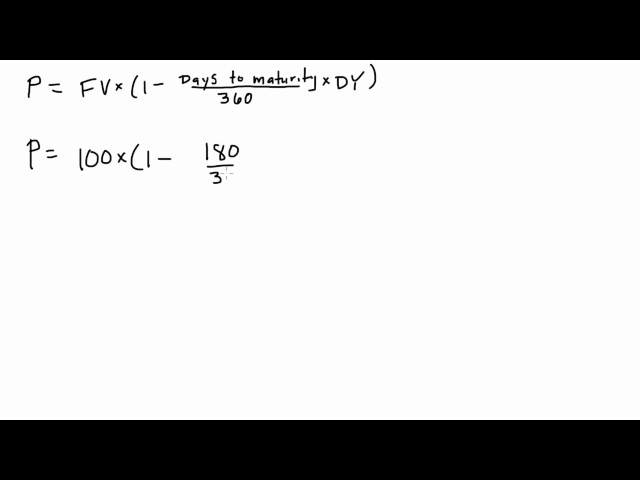The discount rate formula for T-bills calculates the rate at which future cash flows are discounted to determine their present value, specifically for Treasury bills.
For example, if you invest $100 in a one-year T-bill with a 5% discount rate, the present value would be $95.24, reflecting the discounted future cash flow of $100.
Understanding the discount rate formula is crucial for investors navigating the financial markets, as it allows them to assess the value of future income streams and make informed investment decisions. Its historical roots can be traced back to the development of time value of money concepts, highlighting its long-standing significance in financial analysis.
The following sections will explore the key components of the discount rate formula, its applications, and practical considerations for investors.
Discount Rate Formula for T-bills
The discount rate formula for T-bills is a crucial aspect of fixed income investing. Its key aspects include:
- Present Value Calculation
- Future Cash Flows
- Discount Rate
- Time Value of Money
- Investment Analysis
- Risk Assessment
- Yield Curve
- T-bill Pricing
Understanding these aspects is essential for investors to accurately value T-bills, assess their risk-return profile, and make informed investment decisions. The discount rate formula helps determine the present value of future cash flows, considering the time value of money and the prevailing interest rate environment. It also plays a vital role in constructing yield curves, which are crucial for understanding interest rate dynamics and predicting future economic conditions.
Present Value Calculation
Present value calculation is a key aspect of the discount rate formula for T-bills, as it determines the present worth of future cash flows. It involves discounting future cash flows by the discount rate to reflect the time value of money.
- Formula: Present Value = Future Cash Flow / (1 + Discount Rate)n
- Time Value of Money: Considers that money today is worth more than the same amount in the future due to its earning potential.
- Discount Rate: The rate used to discount future cash flows, typically based on prevailing interest rates or the yield curve.
- Example: A $100 T-bill maturing in one year with a 5% discount rate has a present value of $95.24.
Understanding present value calculation is crucial for investors to assess the value of T-bills and make informed investment decisions. It allows them to compare T-bills with other investment options and determine their potential return on investment. Additionally, present value calculation plays a vital role in portfolio management and financial planning, helping investors plan for future financial goals and mitigate risks.
Future Cash Flows
Future cash flows are a critical component of the discount rate formula for T-bills, as they represent the anticipated payments that investors will receive in the future. Understanding these cash flows is crucial for accurate valuation and investment decision-making.
- Principal Repayment: The face value of the T-bill, which is repaid to the investor at maturity.
- Interest Payments: T-bills do not pay periodic interest payments. Instead, the difference between the purchase price and the maturity value represents the implied interest earned.
- Maturity Date: The date on which the T-bill matures and the investor receives the principal repayment.
- Expected Inflation: Investors need to consider the impact of inflation on future cash flows, as it can erode the purchasing power of the principal and interest payments.
By carefully considering these aspects of future cash flows, investors can accurately assess the present value of T-bills and make informed investment decisions. It is important to note that the discount rate used in the formula reflects the time value of money and the prevailing interest rate environment, which can influence the present value calculation.
Discount Rate
In the context of T-bills, the discount rate is the key determinant of their present value and a crucial component of the discount rate formula. It represents the rate at which future cash flows are discounted to reflect their present worth, considering the time value of money and the prevailing interest rate environment.
The discount rate plays a pivotal role in the discount rate formula for T-bills. By incorporating the discount rate, the formula accurately calculates the present value of the future cash flows associated with the T-bill, including the principal repayment and implied interest earned. This calculation is essential for investors to assess the attractiveness and potential return of T-bill investments.
Real-life examples of the discount rate’s impact on T-bill pricing are evident in the financial markets. When interest rates rise, the discount rate used in the formula increases, leading to a decrease in the present value of T-bills. Conversely, when interest rates fall, the discount rate decreases, resulting in an increase in the present value of T-bills. This inverse relationship highlights the significance of the discount rate in determining T-bill valuations.
Understanding the connection between the discount rate and the discount rate formula for T-bills empowers investors with the knowledge to make informed investment decisions. By carefully considering the prevailing interest rate environment and the impact of the discount rate on T-bill valuations, investors can optimize their investment strategies and mitigate potential risks. This understanding is particularly valuable in fixed income investing, where T-bills play a significant role in portfolio diversification and risk management.
Time Value of Money
The “time value of money” concept is fundamentally intertwined with the “discount rate formula for T-bills.” It acknowledges that the value of money today differs from its value in the future due to its earning potential over time. This principle serves as the cornerstone for determining the present value of future cash flows associated with T-bills.
- Present vs. Future Value: The time value of money underscores that a certain amount of money today is worth more than the same amount in the future because of its potential to generate returns or interest over time.
- Impact of Inflation: The time value of money also considers the corrosive effects of inflation, which can erode the purchasing power of money over time. As a result, future cash flows need to be adjusted to account for inflation’s impact.
- Discounting Future Cash Flows: The discount rate formula for T-bills incorporates the time value of money by discounting future cash flows back to the present. This process involves applying a discount rate that reflects the prevailing interest rates and inflation expectations.
- Investment Decisions: Understanding the time value of money is crucial for investors when evaluating T-bills and making investment decisions. It helps them assess the present value of future cash flows and compare different investment options based on their time-adjusted returns.
In essence, the time value of money within the discount rate formula for T-bills provides a framework for valuing future cash flows in the present, taking into account the impact of interest rates, inflation, and the opportunity cost of capital. This concept empowers investors to make informed investment decisions and optimize their returns in the context of fixed income investments.
Investment Analysis
Investment analysis is a critical component of the discount rate formula for T-bills, as it provides the foundation for determining the appropriate discount rate to apply when calculating the present value of future cash flows. Without a thorough understanding of investment analysis, investors may struggle to accurately assess the value of T-bills and make informed investment decisions.
One of the key challenges in investment analysis is determining the appropriate discount rate to use. The discount rate should reflect the time value of money, the riskiness of the investment, and the investor’s opportunity cost of capital. By carefully considering these factors, investors can ensure that the discount rate they use is appropriate for their individual circumstances and investment goals.
Real-life examples of investment analysis within the discount rate formula for T-bills include the use of the yield curve to determine the appropriate discount rate. The yield curve plots the relationship between interest rates and maturities for different types of fixed income securities. By using the yield curve, investors can identify the current market discount rate for T-bills of different maturities. This information can then be used to calculate the present value of future cash flows and make informed investment decisions.
Understanding the connection between investment analysis and the discount rate formula for T-bills is crucial for investors looking to optimize their fixed income investments. By carefully considering the factors that influence the discount rate, investors can make informed decisions about the appropriate discount rate to use, ultimately leading to more accurate valuations of T-bills and better investment outcomes.
Risk Assessment
Risk assessment plays a critical role in the discount rate formula for T-bills, as it helps investors evaluate the potential risks associated with investing in these securities and make informed decisions. By carefully considering the various risk factors, investors can mitigate potential losses and optimize their investment strategies.
- Inflation Risk: The risk that inflation will erode the purchasing power of future cash flows, reducing the real return on investment. For example, if inflation is higher than expected, the present value of future cash flows will be lower, potentially leading to losses.
- Interest Rate Risk: The risk that interest rates will change, affecting the value of T-bills. If interest rates rise, the present value of future cash flows from T-bills will decrease, potentially leading to losses.
- Default Risk: The risk that the issuer of the T-bill will default on its obligation to repay the principal. While T-bills issued by the U.S. government are considered very low risk, there is always a possibility of default, especially in the case of T-bills issued by other countries or entities.
- Liquidity Risk: The risk that T-bills cannot be easily sold or converted into cash when needed. T-bills are generally considered liquid investments, but there may be times when market conditions make it difficult to sell T-bills quickly at a fair price.
These are just a few of the key risk factors that investors should consider when evaluating T-bills and using the discount rate formula to calculate their present value. By carefully assessing these risks, investors can make more informed investment decisions and mitigate potential losses.
Yield Curve
Yield curve plays a critical role in the context of the discount rate formula for T-bills, as it serves as a valuable tool for investors to assess the relationship between interest rates and maturities. By analyzing the yield curve, investors can gain insights into the current and expected future interest rate environment, which is essential for determining the appropriate discount rate to use when calculating the present value of future cash flows from T-bills.
- Term Structure of Interest Rates: The yield curve represents the graphical representation of the relationship between interest rates and the maturities of fixed income securities, providing a snapshot of the term structure of interest rates at a specific point in time.
- Market Expectations: The yield curve reflects the market’s expectations about future interest rates. By analyzing the slope and shape of the yield curve, investors can infer market sentiment and make informed predictions about the direction of future interest rates.
- Discount Rate Determination: The yield curve is a key input in determining the appropriate discount rate to use in the discount rate formula for T-bills. Investors often use the yield curve to identify the current market discount rate for different maturities, which can then be used to calculate the present value of future cash flows.
- Risk Assessment: The yield curve can also be used to assess the risk associated with investing in T-bills. For example, an upward sloping yield curve typically indicates that investors expect interest rates to rise in the future, which can lead to potential losses for investors holding T-bills with longer maturities.
In summary, the yield curve is an indispensable tool for investors seeking to accurately value T-bills using the discount rate formula. By carefully analyzing the yield curve, investors can gain insights into the term structure of interest rates, market expectations, and potential risks, enabling them to make informed investment decisions and optimize their returns.
T-bill Pricing
T-bill pricing is a cornerstone of the discount rate formula for T-bills. By delving into the intricacies of T-bill pricing, investors can gain a comprehensive understanding of how T-bills are valued and the factors that influence their pricing.
- Maturity Date: The maturity date of a T-bill significantly impacts its price. T-bills with longer maturities typically have higher yields and, consequently, higher prices.
- Interest Rate Environment: T-bill pricing is heavily influenced by the prevailing interest rate environment. When interest rates rise, T-bill prices tend to fall, and vice versa.
- Inflation Expectations: Inflation expectations play a role in T-bill pricing, as investors anticipate the impact of inflation on the purchasing power of future cash flows.
- Market Liquidity: The liquidity of the T-bill market affects its pricing. Higher liquidity generally leads to tighter bid-ask spreads and more efficient pricing.
Understanding these factors is crucial for investors to accurately value T-bills using the discount rate formula. By incorporating these considerations into their analysis, investors can make informed investment decisions and optimize their returns in the fixed income market.
Discount Rate Formula for T-bills FAQs
This section provides answers to frequently asked questions (FAQs) about the discount rate formula for T-bills, covering key concepts and practical considerations.
Question 1: What is the discount rate formula for T-bills?
Answer: The discount rate formula for T-bills calculates the present value of future cash flows received from a T-bill investment, considering the time value of money and prevailing interest rates.
Question 2: How is the discount rate determined?
Answer: The discount rate is typically based on the yield curve, which represents the relationship between interest rates and maturities for different fixed income securities, including T-bills.
Question 3: What factors influence T-bill pricing?
Answer: T-bill pricing is influenced by factors such as the maturity date, interest rate environment, inflation expectations, and market liquidity.
Question 4: Why is it important to consider the time value of money when calculating the present value of T-bills?
Answer: The time value of money recognizes that the value of money changes over time due to its earning potential. Ignoring this concept can lead to inaccurate valuations of future cash flows.
Question 5: How can investors use the discount rate formula to make investment decisions?
Answer: The discount rate formula helps investors assess the potential return on T-bill investments by calculating the present value of future cash flows. This information can be used to compare T-bills with other investment options.
Question 6: What are the limitations of the discount rate formula?
Answer: While the discount rate formula provides a valuable tool for valuing T-bills, it has limitations, such as its reliance on accurate estimates of the discount rate and its assumption of constant interest rates over the investment horizon.
In summary, understanding the discount rate formula for T-bills is essential for investors seeking to accurately value and make informed investment decisions in the fixed income market. It is important to consider the various factors that influence T-bill pricing and the limitations of the formula to ensure its effective use.
The following section will delve deeper into practical applications of the discount rate formula for T-bills, providing investors with strategies and examples to enhance their investment decision-making process.
TIPS for Utilizing the Discount Rate Formula for T-bills
This section provides practical tips and strategies for investors to effectively use the discount rate formula for T-bills in their investment decision-making process.
Tip 1: Understand the Time Value of Money: Recognize that the value of money changes over time due to its earning potential. This concept is fundamental to accurately valuing T-bills and should not be overlooked.
Tip 2: Choose an Appropriate Discount Rate: The discount rate should reflect the current market conditions, interest rate environment, and the riskiness of the T-bill investment. Consider using the yield curve as a reference point for determining the appropriate discount rate.
Tip 3: Consider Inflation Expectations: Inflation can erode the purchasing power of future cash flows. Take into account inflation expectations when selecting the discount rate to ensure an accurate assessment of T-bill value.
Tip 4: Analyze the Yield Curve: The yield curve provides insights into the relationship between interest rates and maturities. By analyzing the yield curve, investors can make informed predictions about future interest rates and adjust their discount rate accordingly.
Tip 5: Calculate the Present Value: Use the discount rate formula to calculate the present value of future cash flows received from a T-bill investment. This value represents the current worth of the investment and can be used to compare different T-bills.
Tip 6: Compare T-bills with Other Investments: The present value calculated using the discount rate formula allows investors to compare T-bills with other fixed income investments, such as bonds or certificates of deposit, to determine the most suitable option.
Tip 7: Monitor Interest Rate Changes: Interest rates can fluctuate over time, impacting the value of T-bills. Regularly monitor interest rate changes and adjust the discount rate accordingly to maintain an accurate valuation.
Tip 8: Seek Professional Advice: If needed, consult with a financial advisor or investment professional to gain further insights into the discount rate formula for T-bills and its application in investment decision-making.
By following these tips, investors can enhance their understanding and effective use of the discount rate formula for T-bills, leading to more informed investment decisions and potentially improved returns.
The following section will conclude the article by highlighting the importance of accurately valuing T-bills and the role of the discount rate formula in this process.
Conclusion
This article delved into the discount rate formula for T-bills, exploring its significance and practical applications in fixed income investing. Key takeaways include:
- The discount rate formula is crucial for valuing T-bills, considering the time value of money and prevailing interest rates.
- Factors such as the maturity date, interest rate environment, inflation expectations, and market liquidity influence T-bill pricing.
- Investors can use the discount rate formula to compare T-bills with other investments and make informed investment decisions.
Accurately valuing T-bills is essential for investors seeking to optimize their returns in the fixed income market. By understanding the discount rate formula and its components, investors can effectively assess the present worth of future cash flows and make well-informed investment choices. Remember, the discount rate formula is a valuable tool, but its effective use requires careful consideration of the underlying factors that influence T-bill pricing.