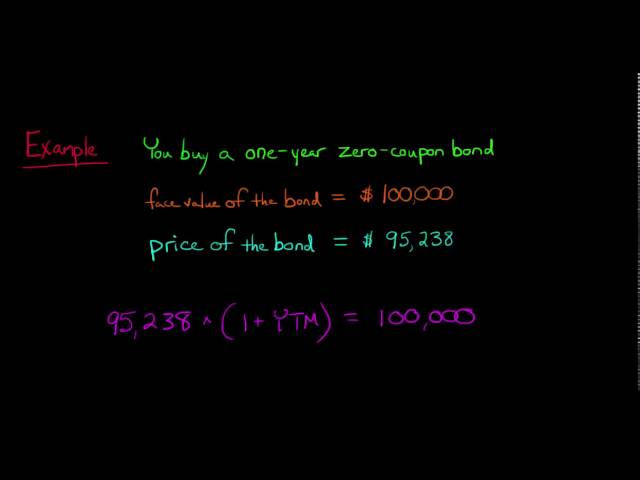Zero rate discount is the noun of the verb “to calculate” and refers to a financial technique used to determine the present value of a future cash flow when the interest rate is assumed to be zero (e.g., forecasting the worth of a given amount of money received in a year without any added interest.).
This concept is important in various financial applications, such as project evaluation, and has been used extensively since its introduction in the 1980s. It provides a simple approach to assessing the present value of future cash flows, ignoring potential variances due to fluctuating interest rates.
This article delves into the details of calculating zero rate discounts and explores its applications in finance and economics.
How to Calculate Zero Rate Discount
Understanding the key aspects of calculating zero rate discount is essential for accurate financial analysis and decision-making.
- Definition
- Formula
- Applications
- Assumptions
- Limitations
These aspects provide a comprehensive framework for comprehending and utilizing zero rate discount in various financial contexts. For instance, understanding the formula allows for precise calculations, while recognizing the limitations helps avoid potential errors.
Definition
The definition of zero rate discount serves as the cornerstone for understanding how to calculate it. It establishes the conceptual framework and provides the necessary context for accurate calculations. Without a clear definition, the calculation process becomes ambiguous and prone to errors.
In practice, the definition guides every step of the calculation. It determines the appropriate formula to use, the variables to consider, and the interpretation of the results. For instance, in the context of project evaluation, the definition clarifies whether the discount rate should be applied to future cash inflows or outflows, ensuring consistency and accuracy in project appraisal.
Moreover, understanding the definition allows for informed decision-making. By comprehending the underlying concepts and assumptions, financial analysts and decision-makers can assess the suitability and limitations of using the zero rate discount method in different situations. This understanding empowers them to make well-reasoned choices that align with the specific goals and constraints of their projects or investments.
Formula
The formula for zero rate discount serves as the backbone of the calculation process. It establishes a precise mathematical relationship between the present value, future value, and the number of periods over which the discount is applied. Without a well-defined formula, calculating zero rate discount would be haphazard and prone to errors.
In its simplest form, the zero rate discount formula is: Present Value = Future Value / (1 + 0%)n, where n represents the number of periods. This formula clearly demonstrates the inverse relationship between present value and the number of periods. As the number of periods increases, the present value decreases, reflecting the time value of money.
Real-life applications of the zero rate discount formula abound in the financial world. For instance, banks use it to determine the present value of future loan payments, enabling them to assess the risk and profitability of lending. Similarly, investors utilize the formula to calculate the present value of expected future dividends or interest payments, guiding their investment decisions.
Understanding the zero rate discount formula is essential for accurate financial analysis and decision-making. It empowers individuals and organizations to make informed choices about investments, loans, and other financial transactions. By mastering this formula, financial professionals can navigate complex financial landscapes with confidence and precision.
Applications
The applications of zero rate discount extend far beyond theoretical calculations, playing a vital role in various financial and economic contexts. Its simplicity and effectiveness have made it a cornerstone for decision-making in diverse industries.
- Valuation
Zero rate discount is used to determine the present value of future cash flows, a key step in valuing companies, projects, and investments. It provides a basis for comparing investment opportunities and making informed decisions about resource allocation.
- Risk Assessment
By incorporating zero rate discount into risk assessment models, analysts can evaluate the potential impact of future events on the present value of assets or projects. This helps in identifying and mitigating risks, enhancing the overall decision-making process.
- Capital Budgeting
Zero rate discount is a fundamental tool in capital budgeting, where it aids in comparing the costs and benefits of different investment projects. It enables businesses to prioritize projects based on their potential returns and make optimal investment decisions.
- Pricing
In the pricing of financial instruments, zero rate discount is used to determine the fair value of bonds, loans, and other debt securities. It helps ensure that the prices reflect the present value of future cash flows, leading to more efficient and transparent markets.
Overall, the applications of zero rate discount are diverse and far-reaching, demonstrating its versatility and importance in the financial world. From valuation to risk assessment and capital budgeting, it serves as a valuable tool for informed decision-making and sound financial management.
Assumptions
Assumptions play a critical role in how to calculate zero rate discount. They establish the underlying conditions and simplifications that make the calculation feasible and meaningful. Without a clear understanding of the assumptions, the results of the discount calculation may be misleading or inaccurate.
One key assumption is that the future cash flows are known with certainty. This assumption allows for a straightforward calculation of the present value, as there is no uncertainty about the timing or amount of the future cash flows. However, in reality, future cash flows are often uncertain, and this uncertainty must be taken into account when calculating the zero rate discount.
Another assumption is that the interest rate is zero. This assumption simplifies the calculation process, as it eliminates the need to consider the impact of compounding interest. In practice, however, interest rates are rarely zero, and the impact of interest must be considered when calculating the present value of future cash flows.
Understanding the assumptions of zero rate discount is essential for its proper application. By carefully considering the assumptions and their implications, financial analysts can make informed decisions about when and how to use this technique.
Limitations
Understanding the limitations of zero rate discount is crucial for its effective application. These limitations stem from the assumptions made in the calculation process and can significantly impact the accuracy and reliability of the results.
One key limitation is the assumption of a zero interest rate. In reality, interest rates fluctuate, and this fluctuation can have a substantial impact on the present value of future cash flows. Ignoring the impact of interest rates can lead to underestimating or overestimating the value of an investment or project.
Another limitation is the assumption of certainty in future cash flows. In practice, future cash flows are often uncertain, and this uncertainty must be taken into account when calculating the present value. Ignoring uncertainty can lead to overly optimistic or pessimistic estimates of the value of an investment or project.
Recognizing the limitations of zero rate discount allows financial analysts to make informed decisions about when and how to use this technique. In situations where interest rates are expected to remain stable and future cash flows are relatively certain, zero rate discount can be a useful tool for approximating the present value of future cash flows. However, in situations where interest rates are expected to fluctuate or future cash flows are uncertain, more sophisticated techniques should be employed.
Frequently Asked Questions on Zero Rate Discount
This FAQ section aims to clarify common questions and address potential misconceptions regarding the calculation of zero rate discount, ensuring a comprehensive understanding of the topic.
Question 1: What is the primary assumption behind zero rate discount?
Answer: Zero rate discount assumes that the interest rate is zero over the period being considered, simplifying the calculation of present value.
Question 2: How does the zero rate discount formula differ from the traditional present value formula?
Answer: The zero rate discount formula omits the interest rate term, as it assumes a zero rate, resulting in a simpler calculation.
Question 3: In what scenarios is zero rate discount most applicable?
Answer: Zero rate discount is suitable when interest rates are expected to remain stable or when future cash flows are relatively certain.
Question 4: What are the limitations of using zero rate discount?
Answer: Zero rate discount does not account for the impact of fluctuating interest rates or uncertainty in future cash flows, which can affect the accuracy of the calculation.
Question 5: How can I incorporate uncertainty into zero rate discount calculations?
Answer: To account for uncertainty, more sophisticated techniques, such as Monte Carlo simulation or scenario analysis, can be employed.
Question 6: What are some real-world applications of zero rate discount?
Answer: Zero rate discount finds applications in project evaluation, bond pricing, and financial planning, among others.
In summary, zero rate discount offers a simplified approach to calculating present value, but its limitations and assumptions should be carefully considered to ensure accurate results. Understanding these nuances is essential for effective application in various financial contexts.
The next section delves into advanced techniques for valuing future cash flows, extending our understanding beyond the zero rate discount method.
Tips for Calculating Zero Rate Discount
This section provides practical tips to enhance the accuracy and effectiveness of zero rate discount calculations.
Tip 1: Define Clear Assumptions: Clearly state the assumptions made regarding interest rates and future cash flows, ensuring transparency and understanding.
Tip 2: Consider Sensitivity Analysis: Perform sensitivity analysis to assess how changes in interest rates and cash flows impact the calculated present value, providing insights into potential risks and uncertainties.
Tip 3: Use Technology Tools: Utilize financial calculators or spreadsheet templates specifically designed for zero rate discount calculations to minimize errors and save time.
Tip 4: Interpret Results Cautiously: Recognize the limitations of zero rate discount and interpret the results with caution, considering alternative valuation methods when appropriate.
Tip 5: Seek Professional Advice: In complex situations or when uncertainty is high, consult with financial professionals to ensure accurate and reliable calculations.
By following these tips, you can enhance the accuracy and reliability of your zero rate discount calculations, leading to more informed financial decisions.
The concluding section of this article will explore advanced techniques for valuing future cash flows, expanding upon the concepts discussed in this section.
Conclusion
This article has explored the intricacies of calculating zero rate discount, highlighting its applications, assumptions, and limitations. The concept of zero rate discount provides a simplified approach to valuing future cash flows by assuming a zero interest rate. However, it is essential to recognize the limitations of this assumption and carefully consider the potential impact of interest rate fluctuations and uncertainty in future cash flows.
By understanding the key aspects of zero rate discount, including its formula, assumptions, limitations, and applications, financial analysts and decision-makers can leverage this technique effectively. It is important to define clear assumptions, perform sensitivity analysis, and interpret results cautiously to ensure accurate and reliable calculations.