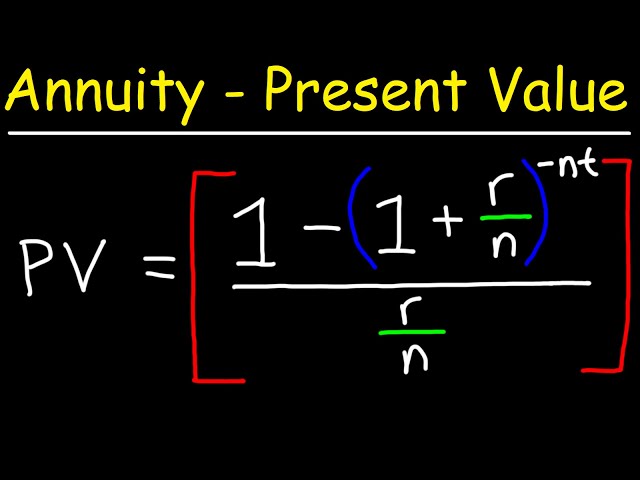Determining the present value of an annuity involves calculating the current worth of a series of future payments, discounted at a specified rate to reflect the time value of money. Consider a scenario where you invest $1,000 annually for the next five years at a 5% discount rate. The present value represents the lump sum you would need today to match the future value of those investments.
Understanding this concept is crucial for informed financial planning, enabling individuals to compare investment options, assess loan values, and plan for retirement. Historically, the development of present value calculations played a significant role in the growth of the financial industry.
In this article, we delve into a step-by-step guide on how to calculate the present value of an annuity, utilizing the discount rate to adjust for the time value of money. We will explore various formulas and provide practical examples to enhance your comprehension and enable you to make sound financial decisions.
How to Calculate Present Value of Annuity with Discount Rate
Accurately calculating the present value of an annuity is crucial for informed financial planning and decision-making. Several key aspects play a vital role in this process:
- Time value of money
- Discount rate
- Annuity payment
- Number of periods
- Present value formula
- Compound interest
- Future value
- Loan amortization
- Investment analysis
Understanding these aspects is essential. The time value of money recognizes that money today is worth more than the same amount in the future due to its earning potential. The discount rate adjusts for this time value, while the annuity payment represents the regular sum received or paid over the specified period. The number of periods determines the duration of the annuity, and the present value formula provides the mathematical framework for the calculation. Compound interest and future value considerations play a role in understanding the growth of the investment over time. Additionally, present value calculations are valuable in loan amortization schedules and investment analysis, enabling individuals to make informed financial choices.
Time Value of Money
The time value of money is a fundamental concept in finance that recognizes the value of money changes over time. It acknowledges that money available today is worth more than the same amount in the future due to its potential earning capacity. This concept is closely intertwined with calculating the present value of an annuity with a discount rate.
Calculating the present value of an annuity involves determining the current worth of a series of future payments. The discount rate, adjusted for the time value of money, is applied to these future payments to calculate their present value. Without considering the time value of money, future payments would be overvalued, leading to inaccurate calculations and potentially poor financial decisions.
A practical example of the time value of money within the context of an annuity is an investment that earns compound interest. The initial investment grows over time due to the interest earned, and the interest earned on the accumulated amount further increases the investment’s value. The present value calculation considers this growth, ensuring that the future value of the annuity is accurately reflected in today’s terms.
Understanding the time value of money and its impact on annuity calculations is crucial for informed financial planning. It enables individuals to make sound investment decisions, compare loan options, and plan for retirement effectively. By incorporating the time value of money into present value calculations, individuals can better assess the true worth of future cash flows and make well-informed choices that align with their financial goals.
Discount rate
When calculating the present value of an annuity, the discount rate plays a crucial role in adjusting for the time value of money. It represents the rate at which future cash flows are discounted to determine their present value, reflecting the opportunity cost of investing the money elsewhere.
- Market interest rates: The prevailing interest rates in the financial market serve as a benchmark for discount rates, influencing the perceived risk and return of investments.
- Inflation: The rate of inflation erodes the purchasing power of money over time, impacting the discount rate used to calculate present value. Higher inflation rates lead to higher discount rates and vice versa.
- Risk premium: Investors typically demand a higher return foring more risk. This risk premium is incorporated into the discount rate, reflecting the perceived uncertainty associated with future cash flows.
- Company-specific factors: For corporate annuities, the discount rate may consider the company’s financial health, industry outlook, and specific project risks.
Understanding the concept of discount rate and its components is crucial for accurate present value calculations. By considering market interest rates, inflation, risk premium, and company-specific factors, individuals and organizations can determine the appropriate discount rate to apply, ensuring informed financial decision-making and sound investment strategies.
Annuity payment
When calculating the present value of an annuity, understanding annuity payments is crucial. An annuity payment refers to each regular installment received or paid over the specified period. It plays a significant role in determining the overall value of the annuity, as it represents the cash flow that is being discounted to its present value.
- Fixed vs. Variable Payments: Annuities can involve fixed payments that remain constant throughout the period or variable payments that fluctuate based on factors like market conditions or inflation.
- Frequency of Payments: Annuity payments can be made annually, semi-annually, quarterly, or even monthly, depending on the agreement or underlying investment.
- Beginning vs. End of Period: Payments can be made at the beginning or end of each period, affecting the calculation of present value due to the time value of money.
- Payment Amount: The amount of each annuity payment is a critical factor in determining the total value of the annuity and its present value.
Considering these aspects of annuity payments is essential for accurate present value calculations. By understanding the nature, timing, and amount of the payments, individuals can better assess the value of an annuity and make informed financial decisions, whether it’s investing in an annuity, planning for retirement, or evaluating loan options.
Number of periods
In calculating the present value of an annuity, the number of periods is a crucial factor that represents the duration or timeframe over which the annuity payments are received or paid. Understanding the nuances of the number of periods is essential for accurate valuations and informed financial decisions.
- Time Horizon: The number of periods determines the time span for which the annuity payments will be received or paid, influencing the overall value of the annuity.
- Frequency of Payments: The number of periods is closely tied to the frequency of annuity payments, whether annually, semi-annually, quarterly, or monthly. This affects the calculation of present value due to the time value of money.
- Maturity Date: The number of periods is directly related to the maturity date of the annuity, which marks the end of the payment period and the final receipt or payment.
- Investment Period: For investment purposes, the number of periods represents the investment horizon or the duration for which the annuity will generate returns.
Understanding these aspects of the number of periods is crucial for accurate present value calculations and effective financial planning. It enables individuals and organizations to evaluate the impact of time, payment frequency, and investment horizon on the value of an annuity, leading to well-informed decisions in various financial contexts.
Present value formula
The present value formula serves as the cornerstone for calculating the present value of an annuity with a discount rate. It establishes the mathematical framework for determining the current worth of a series of future payments, adjusted for the time value of money. Understanding this formula is crucial for accurate financial planning and decision-making.
The present value formula incorporates the discount rate, annuity payment, and number of periods to calculate the present value. The discount rate, representing the opportunity cost of investing elsewhere, is applied to future payments to reflect their current worth. The annuity payment represents the regular cash flow, and the number of periods signifies the duration over which the payments will be received or paid.
In practice, the present value formula finds applications in various financial contexts. For example, it is used to evaluate investment opportunities by comparing the present value of future returns with the initial investment. Additionally, it plays a vital role in loan amortization schedules, determining the periodic payments required to repay a loan while considering the time value of money.
Comprehending the relationship between the present value formula and calculating the present value of an annuity with a discount rate is essential for informed financial decision-making. It enables individuals and organizations to assess the true worth of future cash flows, compare investment options, and plan for financial goals effectively.
Compound interest
Compound interest plays a pivotal role in calculating the present value of an annuity with a discount rate. It refers to the interest earned not only on the principal amount but also on the accumulated interest from previous periods. This has a significant impact on the present value calculation, particularly for long-term annuities.
The discount rate, which adjusts for the time value of money, affects the present value of future annuity payments. However, when compound interest is considered, the growth of the annuity over time is accelerated due to the snowball effect of interest on interest. This means that the present value of an annuity with compound interest will be higher than that of an annuity with simple interest, assuming all other factors remain constant.
A practical example of compound interest in the context of annuity present value calculation is an investment that earns interest annually. The initial investment grows not only due to the interest earned in the first year but also due to the interest earned on the accumulated amount in subsequent years. This exponential growth significantly increases the future value of the annuity, which in turn affects its present value.
Understanding the connection between compound interest and the present value of an annuity with a discount rate is crucial for informed financial planning and decision-making. It enables individuals and organizations to accurately assess the impact of compound interest on long-term investments, compare different annuity options, and make well-informed choices that align with their financial goals.
Future value
Future value plays a pivotal role in calculating the present value of an annuity with a discount rate. It represents the value of an investment or a series of payments at a specified future date, taking into account the effects of compound interest and inflation.
The present value of an annuity is calculated by discounting the future value of each payment back to the present day. The discount rate used in this calculation reflects the time value of money and the opportunity cost of investing elsewhere. By understanding the relationship between future value and the present value of an annuity with a discount rate, individuals can make informed financial decisions and plan for the future effectively.
A practical example of the connection between future value and present value can be seen in retirement planning. When saving for retirement, individuals need to estimate the future value of their investments to determine how much they need to contribute today. By considering the expected rate of return and the time horizon, they can calculate the present value of their future retirement income and adjust their savings plan accordingly.
Understanding the interplay between future value and the present value of an annuity with a discount rate is essential for various financial applications, including investment analysis, loan amortization schedules, and pension planning. It empowers individuals and organizations to make informed choices that align with their long-term financial goals.
Loan amortization
Understanding loan amortization is crucial when calculating the present value of an annuity with a discount rate. Loan amortization refers to the process of spreading the repayment of a loan over regular installments, each consisting of both principal and interest payments. This process affects the present value calculation as it determines the timing and amount of future payments.
- Loan Term: The loan term represents the duration over which the loan is repaid, impacting the number of payments and the calculation of present value.
- Interest Rate: The interest rate charged on the loan directly influences the amount of interest paid each period and, consequently, the present value of the annuity.
- Payment Frequency: Whether payments are made monthly, quarterly, or annually affects the calculation of present value due to the time value of money.
- Amortization Schedule: This schedule outlines the breakdown of each payment into principal and interest components, providing a detailed view of the loan repayment process.
In summary, loan amortization involves understanding the loan term, interest rate, payment frequency, and amortization schedule. These factors collectively influence the present value calculation of an annuity with a discount rate. By considering loan amortization, individuals can accurately assess the impact of different loan options, plan for future expenses, and make informed financial decisions.
Investment analysis
Within the realm of calculating the present value of an annuity with a discount rate, investment analysis plays a pivotal role. It involves evaluating potential investments to determine their viability and expected returns, a crucial step in making sound financial decisions.
- Risk Assessment: Investment analysis involves assessing the level of risk associated with an investment, considering factors like market volatility and the financial health of the underlying company or asset.
- Return Potential: Analysts evaluate the potential return on investment, taking into account factors like interest rates, dividends, and capital appreciation.
- Time Horizon: The time horizon of an investment is a key consideration, as it affects the present value calculation and the overall investment strategy.
- Diversification: Investment analysis also considers diversification strategies to reduce risk, such as investing in a mix of asset classes or geographic regions.
By incorporating investment analysis into the present value calculation, investors can make informed decisions about allocating their funds, balancing risk and return, and achieving their financial goals. It provides a comprehensive framework for evaluating investment opportunities and determining whether they align with the investor’s risk tolerance and time horizon.
Frequently Asked Questions
This section addresses common questions and clarifies aspects of calculating the present value of an annuity with a discount rate to enhance your understanding.
Question 1: What is the significance of the discount rate in present value calculations?
Answer: The discount rate adjusts for the time value of money, reflecting the opportunity cost of investing elsewhere. It ensures that future cash flows are appropriately discounted to determine their present value.
Question 2: How does the number of periods impact the present value?
Answer: The number of periods represents the duration over which annuity payments are received or paid. Longer periods lead to a lower present value due to the compounding effect of the discount rate.
Question 3: What is the role of compound interest in present value calculations?
Answer: Compound interest allows for the calculation of future value, considering the interest earned on both the principal and accumulated interest. This impacts the present value, as future payments are discounted back to the present using the compound interest rate.
Question 4: How does loan amortization relate to present value calculations?
Answer: Loan amortization involves determining the regular payments for a loan, including principal and interest. This directly affects the present value calculation, as it determines the timing and amount of future payments.
Question 5: What are the key considerations in investment analysis when calculating present value?
Answer: Investment analysis involves assessing risk, return potential, time horizon, and diversification strategies. These factors influence the present value calculation, helping investors make informed investment decisions.
Question 6: How does the present value of an annuity differ from its future value?
Answer: The present value represents the current worth of future annuity payments, discounted to reflect the time value of money. In contrast, the future value represents the value of those payments at a specified future date, considering interest and inflation.
These FAQs provide a comprehensive overview of the key concepts and considerations involved in calculating the present value of an annuity with a discount rate. Understanding these concepts is essential for making informed financial decisions and achieving your financial goals.
In the following section, we will delve into practical examples and step-by-step walkthroughs to illustrate the application of these concepts in real-world scenarios.
Tips for Calculating the Present Value of Annuity with Discount Rate
To enhance your understanding of present value calculations, here are several practical tips:
Tip 1: Determine the appropriate discount rate by considering market interest rates, inflation, and risk factors.
Tip 2: Clearly define the number of periods over which annuity payments will be received or paid.
Tip 3: Use the present value formula to calculate the present value, ensuring accurate discounting of future payments.
Tip 4: Consider the effects of compound interest when calculating the present value, especially for long-term annuities.
Tip 5: Understand the relationship between present value and future value to make informed financial decisions.
Tip 6: Apply present value calculations to loan amortization schedules to determine periodic payments and plan for debt repayment.
Tip 7: Utilize present value analysis in investment decisions to compare options and assess potential returns.
By following these tips, you can effectively calculate the present value of an annuity with a discount rate, enabling you to make well-informed financial choices and achieve your financial goals.
In the concluding section of this article, we will explore practical applications of present value calculations in various financial contexts, further solidifying your understanding of this fundamental concept.
Conclusion
This article has provided a comprehensive guide on calculating the present value of an annuity with a discount rate, exploring its significance and practical applications. Key concepts such as time value of money, discount rate, annuity payment, and number of periods have been thoroughly examined.
The interplay between these elements is crucial for accurate present value calculations. The discount rate adjusts for the time value of money, while the annuity payment and number of periods determine the cash flow and duration of the annuity. Understanding these interconnections is essential for informed financial planning and decision-making.
Whether you are evaluating investment opportunities, planning for retirement, or assessing loan options, calculating the present value of an annuity empowers you to make sound financial choices. By incorporating the principles outlined in this article, you can confidently navigate complex financial scenarios and achieve your long-term financial goals.