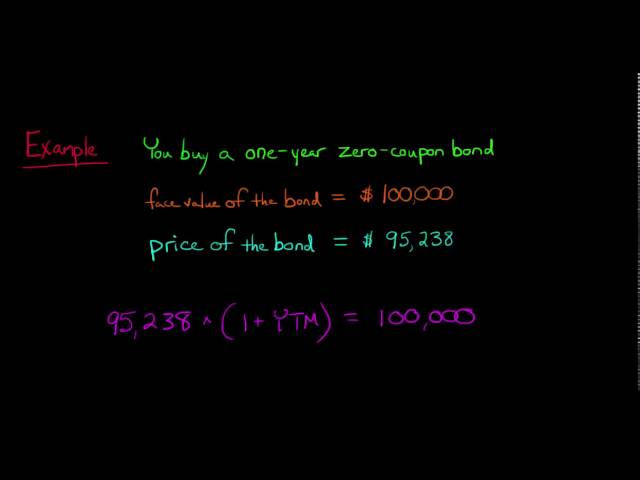How to Calculate a Zero Coupon Bond is the process of determining the present value of a bond that does not pay regular interest payments, also known as a zero-coupon bond.
Understanding how to calculate a zero coupon bond is essential for investors seeking alternative investment strategies. Zero-coupon bonds offer unique advantages, including potential tax benefits and diversification opportunities.
In this comprehensive guide, we will explore the formula, factors, and practical applications of calculating the present value of zero-coupon bonds, empowering you to make informed investment decisions.
How to Calculate a Zero Coupon Bond
Calculating the present value of a zero-coupon bond involves several key aspects, each playing a vital role in determining its value.
- Face Value
- Maturity Date
- Yield to Maturity
- Time to Maturity
- Present Value
- Compounding Frequency
- Tax Implications
- Investment Horizon
Understanding these aspects allows investors to accurately value zero-coupon bonds, assess their risk-return profile, and make informed investment decisions. For example, the yield to maturity influences the present value, while the investment horizon determines the suitability of the bond within an investor’s portfolio.
Face Value
The face value of a zero-coupon bond represents its maturity value, which is the amount an investor receives upon the bond’s maturity date.
- Nominal Value: The face value represents the principal amount of the bond that the investor initially invests.
- Maturity Amount: At the end of the bond’s term, the investor receives the face value, which is the bond’s maturity amount.
- Present Value: The face value, along with the yield to maturity and time to maturity, is used to calculate the present value of the bond.
- Tax Implications: In some cases, the face value may be subject to taxation upon maturity, which can impact the investor’s overall return.
Understanding the face value is crucial for investors to accurately assess the potential return and risk associated with zero-coupon bonds, enabling them to make informed investment decisions.
Maturity Date
The maturity date of a zero-coupon bond is a crucial factor in its valuation and return calculation. It represents the specific date on which the bond matures and the investor receives the face value.
- Bond Term: The maturity date determines the duration of the bond, which influences its risk and return profile.
- Present Value Impact: The time to maturity, calculated from the present date to the maturity date, is a key input in the formula to calculate the present value of the bond.
- Yield to Maturity: The yield to maturity, which represents the annualized rate of return an investor can earn by holding the bond until maturity, is directly affected by the maturity date.
- Tax Implications: In some cases, the maturity date may trigger tax implications, such as capital gains or income tax, which can impact the investor’s overall return.
Understanding the maturity date empowers investors to assess the potential return, risk, and tax implications associated with zero-coupon bonds, enabling them to make informed investment decisions.
Yield to Maturity
Understanding yield to maturity (YTM) is vital in calculating the present value of a zero-coupon bond. YTM is the annualized rate of return an investor earns if they hold the bond until maturity.
- Determination: YTM is calculated using the present value formula, considering the bond’s face value, time to maturity, and present value.
- Market Conditions: YTM is influenced by market interest rates, economic conditions, and the perceived risk associated with the bond.
- Impact on Bond Price: Changes in YTM lead to corresponding changes in the bond’s price. Higher YTMs result in lower bond prices, and vice versa.
- Investment Strategy: YTM is a key factor in investment decisions, as it helps investors compare potential returns and make informed choices.
In summary, yield to maturity plays a critical role in determining the value and return of a zero-coupon bond. It serves as a benchmark against which investors can assess investment opportunities and make informed decisions aligned with their financial goals.
Time to Maturity
In the context of “how to calculate a zero coupon bond,” time to maturity plays a pivotal role in determining its present value and return. It refers to the duration between the bond’s issuance date and its maturity date, influencing various aspects of the bond’s valuation and investment strategy.
- Investment Horizon: Time to maturity should align with the investor’s investment horizon. Matching the bond’s maturity date to the investor’s financial goals ensures optimal returns.
- Interest Rate Risk: Longer time to maturity exposes the bond to interest rate fluctuations, leading to potential price volatility. Investors must assess their risk tolerance and market outlook.
- Present Value: Time to maturity is a key determinant in calculating the present value of the zero-coupon bond. A longer time to maturity typically results in a lower present value due to the time value of money.
- Yield to Maturity: Time to maturity is inversely related to yield to maturity. As time to maturity increases, yield to maturity generally decreases, and vice versa.
Understanding the implications of time to maturity empowers investors to make informed decisions when calculating the present value of zero-coupon bonds. Accurately assessing the duration of the investment and its alignment with financial goals is crucial for maximizing returns and managing risk.
Present Value
In the context of “how to calculate a zero coupon bond,” present value (PV) plays a central role in determining its worth. PV represents the current value of the bond, considering its future maturity value and the time value of money. Understanding this relationship is crucial for accurate bond valuation and informed investment decisions.
Present value is a critical component of “how to calculate a zero coupon bond” because it allows investors to compare the bond’s current worth to its future value at maturity. By discounting the future maturity value back to the present using an appropriate discount rate, investors can assess the bond’s attractiveness relative to other investment options.
Real-life examples demonstrate the practical applications of present value in bond calculations. For instance, if a zero-coupon bond has a face value of $1,000 and matures in 10 years, and the current market interest rate is 5%, the present value of the bond would be approximately $613.91. This calculation considers the time value of money, which reduces the future value to its current equivalent.
In summary, understanding the relationship between present value and “how to calculate a zero coupon bond” empowers investors with valuable insights. It enables them to accurately assess bond value, compare investment options, and make informed decisions that align with their financial goals.
Compounding Frequency
In the realm of “how to calculate a zero coupon bond,” compounding frequency holds significant relevance, influencing the overall valuation and return of the bond. Compounding refers to the addition of interest to both the principal amount and the previously accumulated interest, leading to an exponential growth of the investment over time.
Zero-coupon bonds do not pay regular interest payments, making compounding frequency a critical component in calculating their present value. The more frequent the compounding, the higher the present value of the bond. This is because more frequent compounding results in a larger accumulated value due to the snowball effect of interest being added to interest.
Real-life examples illustrate the practical implications of compounding frequency in “how to calculate a zero coupon bond.” Consider two zero-coupon bonds with identical face values and maturity dates. If one bond compounds annually and the other compounds semi-annually, the bond with semi-annual compounding will have a higher present value due to the more frequent accumulation of interest.
In summary, understanding the relationship between compounding frequency and “how to calculate a zero coupon bond” is crucial for investors seeking accurate bond valuation and optimal returns. By considering the impact of compounding frequency, investors can make informed investment decisions that align with their financial goals and risk tolerance.
Tax Implications
In the realm of “how to calculate a zero coupon bond,” tax implications play a significant role, affecting the overall return and investment strategy. Understanding the relationship between tax implications and bond calculations is crucial for investors seeking to optimize their financial outcomes.
Tax implications arise primarily due to the unique nature of zero-coupon bonds, which do not pay regular interest payments. Instead, the return on investment is realized upon maturity when the investor receives the face value of the bond. This lump-sum payment is subject to taxation, depending on the investor’s tax bracket and the bond’s holding period.
Real-life examples illustrate the practical impact of tax implications on “how to calculate a zero coupon bond.” Consider an investor who purchases a zero-coupon bond with a face value of $1,000 and a maturity date in 10 years. If the bond is held until maturity, the investor will receive $1,000, which is subject to capital gains tax. The applicable tax rate will depend on the investor’s tax bracket and whether the bond was held for more than one year.
In summary, understanding the relationship between tax implications and “how to calculate a zero coupon bond” is essential for investors to make informed decisions. By considering the tax implications, investors can accurately assess the potential return on their investment and plan their financial strategies accordingly.
Investment Horizon
In the context of “how to calculate a zero coupon bond,” investment horizon plays a prominent role in determining the bond’s suitability and potential return for an investor. It refers to the period over which an investor plans to hold the bond until maturity.
- Matching Maturity: Investors should align the bond’s maturity date with their investment horizon to optimize returns and minimize reinvestment risk.
- Interest Rate Risk: Longer investment horizons expose the bond to interest rate fluctuations, potentially affecting its value. Investors with shorter horizons are less susceptible to these fluctuations.
- Tax Implications: The investment horizon influences the tax treatment of the bond’s return. Holding the bond for more than one year may qualify for favorable tax rates.
- Personal Circumstances: Individual circumstances, such as retirement plans or financial goals, should be considered when determining the appropriate investment horizon.
Understanding the relationship between investment horizon and “how to calculate a zero coupon bond” is essential for investors to make informed decisions. By considering the potential implications for return, risk, and tax treatment, investors can determine the optimal investment strategy and select bonds that align with their financial objectives.
Frequently Asked Questions
This FAQ section provides concise answers to common questions regarding “how to calculate a zero coupon bond.” These questions aim to address potential queries and clarify important aspects, ensuring a comprehensive understanding of the topic.
Question 1: What is the key difference between a zero-coupon bond and a traditional coupon bond?
Answer: Zero-coupon bonds do not pay periodic interest payments like traditional coupon bonds. Instead, they are issued at a discount to their face value and pay the full amount at maturity.
Question 2: How is the present value of a zero-coupon bond calculated?
Answer: The present value is calculated using the formula: PV = FV / (1 + r)^n, where PV is the present value, FV is the face value, r is the yield to maturity, and n is the number of years to maturity.
Question 3: What factors influence the yield to maturity (YTM) of a zero-coupon bond?
Answer: YTM is affected by market interest rates, the creditworthiness of the issuer, and the time to maturity of the bond.
Question 4: Are zero-coupon bonds affected by interest rate fluctuations?
Answer: Yes, zero-coupon bonds are sensitive to interest rate changes, particularly those with longer maturities. Rising interest rates can lead to a decrease in bond prices.
Question 5: What are the tax implications of investing in zero-coupon bonds?
Answer: Zero-coupon bonds are subject to capital gains tax upon maturity. The tax treatment depends on the holding period and the investor’s tax bracket.
Question 6: How can I use zero-coupon bonds in my investment portfolio?
Answer: Zero-coupon bonds offer diversification and potential for capital appreciation. They can be used to meet specific financial goals, such as funding retirement or saving for education.
These FAQs provide a foundation for understanding “how to calculate a zero coupon bond.” For further insights into bond valuation, risk assessment, and investment strategies, continue reading the comprehensive article.
Tips for Calculating Zero Coupon Bonds
This section provides practical tips to assist you in accurately calculating zero coupon bonds, ensuring a comprehensive understanding of the process.
Tip 1: Determine Key Inputs: Gather essential information, including the bond’s face value, maturity date, and yield to maturity (YTM).
Tip 2: Use a Financial Calculator: Leverage financial calculators or online tools specifically designed for bond calculations to simplify and expedite the process.
Tip 3: Consider Compounding Frequency: Account for the frequency of compounding, as it directly affects the present value of the bond.
Tip 4: Understand Tax Implications: Be mindful of the tax implications associated with zero-coupon bonds, as they may impact your overall return.
Tip 5: Assess Market Conditions: Monitor market interest rates and economic conditions, as they influence the YTM and bond prices.
Tip 6: Calculate Present Value: Utilize the formula PV = FV / (1 + r)^n to accurately calculate the bond’s present value, considering the time to maturity.
Tip 7: Compare Bonds: Evaluate different zero-coupon bonds based on their present values and yields to select the most suitable investment option.
Tip 8: Consult a Financial Advisor: Seek professional guidance from a financial advisor for personalized advice and assistance in incorporating zero-coupon bonds into your investment portfolio.
By following these tips, you can effectively calculate zero coupon bonds, assess their potential returns, and make informed investment decisions aligned with your financial goals.
The insights gained from these tips will serve as a solid foundation as we delve into the conclusion of this comprehensive guide to “How to Calculate a Zero Coupon Bond.”
Conclusion
This comprehensive guide has delved into the intricacies of “how to calculate a zero coupon bond,” providing valuable insights for investors seeking to navigate the unique characteristics of this fixed-income instrument.
Key considerations include the bond’s face value, maturity date, yield to maturity, time to maturity, compounding frequency, and tax implications. Understanding the interplay between these factors empowers investors to accurately calculate the present value of zero-coupon bonds and make informed investment decisions.